[科普中国]-平行平面定理

平行平面定理(theorem of parallel planes)是立体几何的重要定理之一。如果一个平面与两个平行平面同时相交，则在形成的三面八角几何图形中：1.同位二面角相等；2.内错二面角相等；3.外错二面角相等；4.同旁内二面角互补；5.同旁外二面角互补。

基本介绍平行平面定理立体几何的重要定理之一，如果一个平面与两个平行平面同时相交，则在形成的三面八角几何图形中:

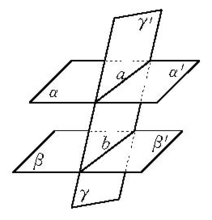
1.同位二面角相等，如图中的；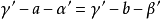

2.内错二面角相等，如图中的；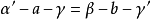

3.外错二面角相等，如图中的；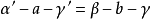

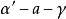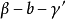4.同旁内二面角互补，如图中的和互补；

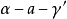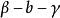5.同旁外二面角互补，如图中的和互补1。

定理的证明一平面和两个平行平面相交，求证它们的同位二面角相等、内错二面角也相等，同旁二面角互补。

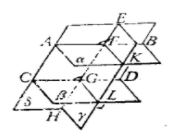
分析：通过作与此三平面垂直的平面，得到平面上的三线八角，转化为平面几何问题证。

证明：如图2，设平面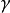和两平行平面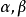相交，交线为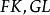，过交线FK上任意一点F作平面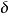使与FK垂直，设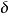平面与平面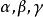的交线分别为AB、CD、EH。

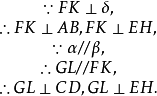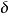则在平面内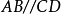，，AB，CD与EH所成的角均为有关二面角的平面角。

由平面几何可知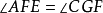，(同位角相等)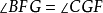，(内!错角相等)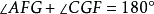，(同旁内角互补)。

而具有相等平面角的两个二面角相等，具有互补平面角的两个二面角互补。

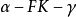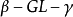所以： 二面角与二面角相等；

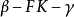二面角与二面角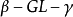相等；

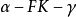二面角与二面角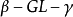互补。

即同位二面角相等，内错二面角相等，同旁二面角互补2。

平行平面的其他定理定理1 如果一个平面平行于两条相交直线，那么这个平面也就平行于这两条相交直线所确定的平面。由这个定理，可以知道：如果一个平面内的两条直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行。

定理2垂直于同一条直线的两个平面平行。

定理3 如果两个平面都平行于第三个平面，那么这两个平面也互相平行。

定理4 如果两个平行平面之一与第三个平面相交，则另一个也与第三个平面相交。

定理5 如果两个平行平面都和第三个平面相交，那么，它们的交线平行。

定理6如果一条直线垂直于两个平行平面中的一个平面，那么这条直线也垂直于另一个平面3。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学