基本介绍定义一
一个多面体的界面是一个柱面和两个平面,而这两个平面不互相平行,则这个多面体叫做截棱柱。如图1,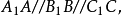 但面
但面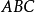 与面
与面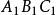 不平行,这个多面体就是一个截棱柱(图1)或截柱体1。
不平行,这个多面体就是一个截棱柱(图1)或截柱体1。
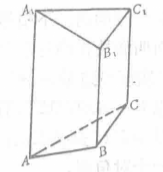
定义二两个互不平行的平面与一个准线是封闭曲线的柱面相交,所围成的形体,我们称它为斜截柱体,它的表面的柱面部分称为侧面,两个平面部分称为端面。
斜截柱体的体积和侧面积计算斜截柱体的体积和侧面积计算一般用重积分和曲线积分计算,有的也可用初等方法计算,但这些方法往往比较复杂。本文介绍一种比较简便的计算方法2。
定理1斜截柱体的体积等于它的直截面(与侧面母线垂直且不与端面相交的截面) 面积与两个端面的重心之间的距离的乘积2。
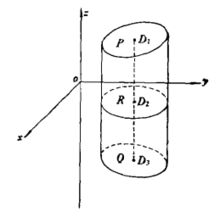
**证明:**如图2,斜截柱体的侧面母线与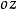 轴平行,P和Q为它的两个端面,R为xoy 平面上的直截面,
轴平行,P和Q为它的两个端面,R为xoy 平面上的直截面,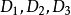 分别是P、R、Q 的重心。
分别是P、R、Q 的重心。
考虑xoy 平面以上的部分: 设上端面P所在平面的方程为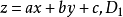 和
和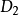 的坐标分别为
的坐标分别为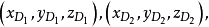 那么
那么
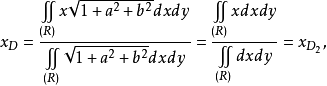 同理,
同理,
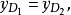 因此,D1D2平行于
因此,D1D2平行于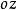 轴,也平行于侧面母线。
轴,也平行于侧面母线。
又因为
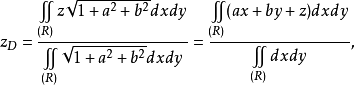 所以,xoy平面以上部分的体积
所以,xoy平面以上部分的体积
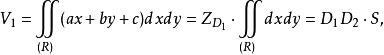 其中,S表示直截面R的面积。
其中,S表示直截面R的面积。
同理可证:xoy平面以下部分的体积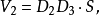 且
且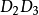 平行
平行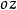 轴。
轴。
所以,该斜截柱体的体积
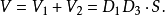 定理1得证。
定理1得证。
推理1斜截三梭柱的体积等于它的直截面面积与三条侧棱的平均长度的乘积。
推理2斜截正棱柱的体积等于它的直截面面积与所有侧棱的平均长度的秉积。
推理1可从定理1得到,也可用初等方法证明。推理2可从定理1和推理1得到,也可以只应用推理1来证明。
定理2斜截柱体的侧面积,等于它的直截面的周界曲线的长度乘以通过该周界曲线的重心且与侧面母线平行的直线被夹在两个端面之间的线段长度的积。
应用举例例1凡斜截四棱柱、斜截五棱柱等都可分割成斜截三棱柱计算坝,可分割成两个斜截三棱柱,即使当基础面倾斜(指与堤坝垂直的方向)时也适用。
例2 图3所示的半圆直角弯管是由两个斜截柱体构成的,我们来计算其中一段的容积(不考虑管壁厚度)和侧面积。
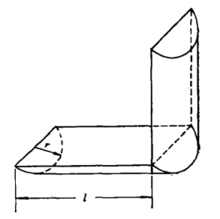
设该段管子的内侧长为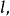 直截面的半径为
直截面的半径为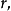 下端面与侧面垂直,上端面与直截面相交成45度角。我们知道半圆面和半圆弧的重心到直径的距离分别为
下端面与侧面垂直,上端面与直截面相交成45度角。我们知道半圆面和半圆弧的重心到直径的距离分别为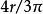 和
和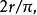 那么根据定理1和定理2,该段管子的容积和侧面积分别为
那么根据定理1和定理2,该段管子的容积和侧面积分别为
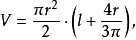 和
和
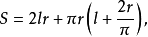 (定理2对准线不是封闭曲线的斜截柱面也适用,因此分两部分计算)。
(定理2对准线不是封闭曲线的斜截柱面也适用,因此分两部分计算)。
由于不少的平面图形和平面曲线的重心是已知的,因此采用这一方法来计算斜截柱体的体积和侧面积往往是比较方便的。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国