[科普中国]-二次不等式

定义

当不等式两端是含有n个(n是自然数)未知数的整式时，则根据整式的次数分别叫做n元一次不等式，n元二次不等式等等。例如，不等式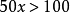 是一元一次不等式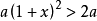， 是一元二次不等式；而不等式 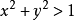则是二元二次不等式。1二次不等式(quadratic inequality)是一种整式不等式，如果整式不等式的次数是2，则称为二次不等式，若二次不等式有n个未知数，则称为n元二次不等式。

一元二次不等式

定义：含有一个未知数，且的未知数的最高次数是二次的不等式叫作一元二次不等式。

一元二次不等式的解法：

(1)一元二次不等式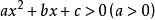，设相应的一元二次方程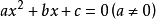的两根为。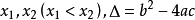

若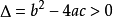，一元二次不等式的解集为；

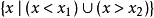若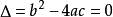，一元二次不等式的解集为；

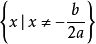若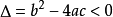，解集为R。

(2)一元二次不等式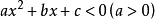，设相应的一元二次方程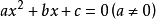的两根为。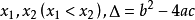

若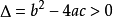，一元二次不等式的解集为；

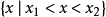若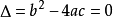，一元二次不等式的解集为；

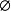若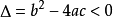，一元二次不等式的解集为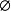。2

二元二次不等式

定义1 一个二元二次方程表示一条圆锥曲线，为简便计，这里只研究具有标准形式(非退化)的圆锥曲线方程所对应的不等式表示的区域。

定义2 平面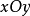上所有满足二元二次不等式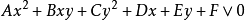(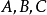不全为零)的点的集合，叫作这个二元二次不等式表示的区域，这里“V”表示“>”，“