[科普中国]-垂足曲面

垂足曲面(pedal surface)是曲面的一种类型。亦称菲涅耳弹性曲面。

菲涅耳(Fresnel，A.J.)在研究光波衍射的规律时所建立的波动曲面理论中给出了垂足曲面的概念。

概念垂足曲面(pedal surface)是曲面的一种类型。亦称菲涅耳弹性曲面。从椭球面：

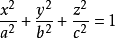的中心到它的切平面作垂线，垂足的轨迹是四次曲面(x2+y2+z2)2=a2x2+b2y2+c2z2。该曲面称为菲涅耳弹性曲面或垂足曲面。菲涅耳(Fresnel，A.J.)在研究光波衍射的规律时所建立的波动曲面理论中给出了垂足曲面的概念。

曲面微分几何研究的主要对象之一。直观上，曲面可以看作是空间具有二个自由度的点的轨迹。数学中通常称曲面是二维拓扑流形，即满足于第二可数公理，且各领域与欧几里得平面的圆的内部同胚的拓扑空间。约公元前300年欧几里得在《几何原本》中给出面的定义：面只有长度和宽度，面的边缘是线。这是对面的最早说明。但同线的概念一样，“长度”、“宽度”等都还没有定义，因此是不完全的定义。古希腊流传下来的朴素概念认为曲线移动可以形成曲面，或立体的表面是曲面等。也有人称不是平面的面为曲面，但在现代数学中曲面有包含平面的意义。

最早研究曲面性质的是古希腊科学家阿基米德，他得到旋转抛物面的一些有趣性质。系统的曲面理论的研究始于17世纪末，最先讨论的是曲面上的测地线。1697年约翰·伯努利提出一凸曲面上求两点间的最短弧问题，第二年雅各布·伯努利解决了柱面、锥面和旋转曲面上的测地线问题。1728年欧拉给出曲面上测地线的微分方程，1760年又在《关于曲面上曲线的研究》中建立了曲面的理论，1771年发表《论表面可以展平的立体》中首次讨论了可展曲面。他的工作由法国数学家蒙日等人进行了发展。蒙日在1802年发表的《代数在几何中的应用》一文中证明了二次曲面的每一个平面截口是一条二次曲线，还证明了单叶双曲面和双曲抛物面是直纹曲面。19世纪射影几何复兴，曲面理论随之发展。1832年瑞士数学家施泰纳利用射影原理造出直纹二次曲面，后来英国数学家凯莱(1849)、德国数学家库默尔(1864)先后给出三次和四次曲面的特别例子。

1827年高斯发表《关于曲面的一般研究》，奠定了曲面论的基础。他研究了曲面的曲率，提出曲面作为一个空间的概念，使曲面的几何可以集中在曲面本身上进行研究。这种思想由黎曼继承并发展，推广到任何空间，其中关于任意n维流形的曲率概念就是高斯关于曲面的总曲率概念的推广。以后匈牙利数学家拉多给出黎曼曲面的一种精确定义，1925年证明了曲面一般可进行单形剖分，从而可与二维多面体同胚的结论。在曲面的整体性质方面，德国数学家麦比乌斯最早发现单侧曲面，将长方形的边扭成180°后与对边粘合得到的麦比乌斯带是不可定向曲面中最著名的例证。曲面理论的进一步结果体现在微分几何学与拓扑学等学科中，其研究方兴未艾。1

微分几何用分析方法研究空间几何性质的数学分支。在古典意义下，微分几何学研究三维欧几里得空间中的曲线和曲面在一点邻近的性质，其发展与分析学和解析几何学的发展不可分割。它起源于17世纪发现微积分之时，函数与函数的导数概念实质上等同于曲线与曲线的斜率，函数积分在几何上解释为一曲线下的面积。牛顿、莱布尼茨对此做了奠基性的工作。法国数学家费马还较早地研究了光滑平面曲线作切线的方法，成为微积分的先驱之一。曲线的法线、拐点、曲率、曲率圆、渐屈线、包络线等平面曲线的微分几何都作为微积分的一部分发展起来，其中荷兰数学家惠更斯的渐屈线研究(1673)、牛顿的曲率中心概念的引入(1671)、约翰·伯努利的包络研究成果(1691)颇具代表性。1696年法国数学家洛必达的《阐明曲线的无穷小分析》出版，帮助完成并传播了平面曲线的理论。1731年法国数学家克莱罗开创空间曲线理论，称之为“双曲率曲线”，研究了空间曲线的切线、弧长表达式等问题。1736年欧拉首先引进平面曲线的内在坐标概念，即以曲线弧长作为曲线上点的坐标，开始曲线的内在几何研究。1745年欧拉出版《无穷分析引论》，介绍了平面和空间图形的微分几何。他将曲率描述为曲线的切线方向和一固定方向的交角相对于弧长的变化率，引进曲面上的法曲率、总曲率、法曲率的欧拉公式及球面映射等。他还于1775年给出关于扭曲线理论的完整论述，并与约翰·伯努利、丹尼尔·伯努利一起探讨测地线，将测地线描述为某些微分方程的解。1760年欧拉在《关于曲面上曲线的研究》中建立了曲面理论，得到欧拉定理等结果，成为微分几何发展的里程碑。后来蒙日不仅创立了画法几何学，还于1807年出版了关于曲线和曲面的第一部独立的著作《分析学在几何中的应用》。他还独立研究了可展曲面的课题，将同一个问题分别置于几何和分析领域进行讨论，并肯定了这样做的好处，振兴了综合几何学。蒙日的学生迪潘在《几何学的发展》(1813)中论述了曲面上的共轭渐近线和迪潘指标线，在《几何学和力学的应用》中推广了蒙日的线汇结果。19世纪中期，弗雷内得出曲线的基本微分方程，被称为弗雷内公式。1887—1898年达布创造空间曲线的活动标架概念，详细讨论了曲面理论和曲线坐标，从而完整地建立起曲线理论。

整体微分几何兴起于20世纪初。德国数学家霍普夫约于1925年起对黎曼空间的微分几何结构与拓扑结构的关系进行研究，后来比利时数学家德·拉姆和英国数学家霍奇对流形上局部性质与整体性质的联系进行了研究，建立了流形上微分结构、拓扑结构及黎曼结构的深刻制约关系。在研究黎曼流形的曲率与拓扑结构之间的联系方面，美国数学家艾伦多弗和法国数学家韦伊与中国—美国数学家陈省身用不同方法将紧致曲面上的高斯一博内公式扩充到高维曲面和紧致黎曼流形上去。陈省身等人还在纤维丛理论中做出突出贡献。法国数学家阿达马和E.嘉当发现单连通的、曲率非正的完备黎曼流形必同胚于欧氏空间Rn，这些都是极富启发性的成果。另外，嵌入问题也引起数学家们的兴趣。美国数学家惠特尼于1936年证明了微分流形的嵌入定理，指出每一个n维的微分流形可以嵌入到一个2n+1维的欧氏空间。另一英国数学家莫利证明了对紧致的实解析流形这个结果也成立。到20世纪50年代，黎曼流形的整体等距嵌入问题也已解决，并对非线性分析和非线性偏微分方程的求解产生重要影响。

现在微分流形是在微分几何与拓扑学两者的观点下发展起来的重要课题，因此，微分几何学可看作是给定二次微分形式、复结构、联络等特殊结构的微分流形的理论，包括中国学者在内的一大批数学家正致力于这方面的研究工作。

人物简介菲涅耳是法国物理学家。1788年5月10日生于法国诺曼底布罗利耶城。在当建筑师的父亲影响下。他中小学时代的学习成绩一直很出众。1806年，菲涅耳在巴黎工艺学校毕业。1809又毕业于巴黎桥梁与公路学校，并获得土木工程师的文凭。此后，长期在法国政府的某些机构中担任工程师。他利用业余时间对光学进行了卓有成效的研究，取得许多科研成果。1823年，法国科学院授予他院士称号。1825年被英国皇家学会选为会员，并在两年后被授予伦福德奖章。1827年7月 14日因患肺病医治无效逝世，年仅39岁。

菲涅耳是从1814年开始研究光学的，他从自己微薄的经济收入中挤出一部分钱来购买供实验用的仪器和设备，研究条件十分艰难，但是他勤奋努力，刻苦钻研，取得了很大成就。他提出了新的惠更斯原理，即惠更斯-菲涅耳原理，完善了光的衍射理论。当 1818年法国科学院悬赏解决衍射问题时，由于菲涅耳在1816年发表的论文就对衍射问题作出了重要的理论论证并有严格实验根据，因此这项奖金终于被菲涅耳所获得。菲涅耳在衍射方面有许多贡献，波动光学中以他姓氏命名的实验和概念有： 菲涅耳圆孔衍射、菲涅耳圆盘衍射、菲涅耳单狭缝衍射、菲涅耳半波带和菲涅耳波带片等。菲涅耳另一个重大贡献是光偏振方面的研究成果。1821年通过偏振对干涉影响的实验肯定了光波是横波。1822年首次发现了圆偏振光和椭圆偏振光，并用波动说解释了偏振面的转动现象。1823年确立了光在反射与折射时的定量定律，即著名的菲涅耳定律。并由此解释了光在反射时发生的偏振现象以及全反射时发生的椭圆偏振现象。他的双折射理论也取得了成功，为晶体光学的建立奠定了基础。菲涅耳提出的地球因运动而部分曳引以太的观点曾产生过很大的影响，他导出了光在相对以太参考系运动的透明物体中的速度公式，即菲涅耳运动介质光速公式。此式为法国物理学家菲佐1851年用实验所证实。菲涅耳还设计过一种阶梯多级透镜系统来改进灯塔的照明，为海运事业的发展作出了重要贡献。2

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学