[科普中国]-凸性

意义

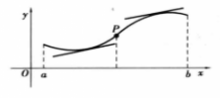
在研究函数图形的变化时，仅仅研究单调性并不能完全反映它的变化规律。如图1，函数虽然在区间[a，b]内单调递增，但却有不同的弯曲状况，从左到右，曲线先是向下凹，通过P点后改变了弯曲方向，曲线向上凸。因此，在研究函数的图形时，除了研究其单调性，对于它的弯曲方向及弯曲方向的改变点的研究也是很有必要的。从图1明显可知，曲线向下凹时，弯曲的弧段位于这弧段上任意一点的切线的上方，曲线向上凸时，弯曲的弧段位于这弧段上任意一点的切线的下方。2

基本概念凹函数和凸函数如果在某区间I内，连续函数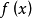 的曲线弧位于其上任意一点切线的上方(下方)，则称曲线在这个区间内是凹的(凸的)，区间I称为函数 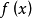的凹区间(凸区间)，记为 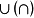，函数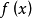 则为区间I上的凹函数(凸函数)。2

凸性的定义连续曲线上，凹曲线和凸曲线的分界点称为曲线的拐点。

曲线的凹或凸统称为曲线的凸性，显然，只要知道了函数的凸性即找到函数的凹凸区间，拐点就显而易得。2

判断曲线的凸性设函数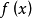 在区间[a，b]上连续，在(a，b)内具有二阶导数，则：

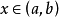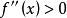①如果 时，恒有 ，则曲线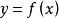 在[a，b]内是凹的；

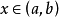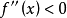②如果 时，恒有 ，则曲线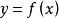 在[a，b]内是凸的。

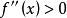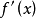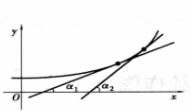
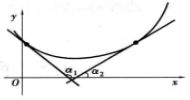
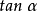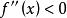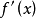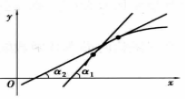
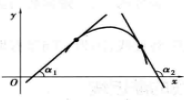
因为 时， 单调增加，即斜率 由小变大，曲线是凹的，如图2、3所示；反之，如果 时， 单调减少，即斜率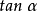 由大变小，曲线是凸的，如图4、5所示。

拐点既然是曲线上凸凹的分界点，故在拐点的左右邻域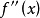 必然异号，而拐点处的二阶导数 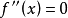或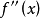 不存在，因此在确定拐点时，首先找到 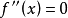或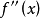 不存在的点，以这些点将定义域划分为若干个子区间，然后检验这些点左右邻域 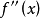的符号，若异号则为拐点，否则不是拐点。2

例题解析例1 求曲线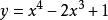 的凹凸区间与拐点。2

解: 易知，定义域为(-∞，+∞)，求导数得

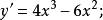
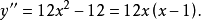
令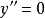 ，得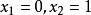 ，且二阶导数没有不存在的点。

以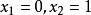 为分界点，将定义域划分为3个子区间，并讨论函数在各子区间上的凸性及拐点，见表1。

|| || 表1

从表1可知，该曲线的凹区间为(一∞，0)，(1，+∞)，凸区间为(0，1)；曲线的拐点为(0，1)和(1，0)。

例2 求曲线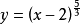 的凹凸区间及拐点。

解： 易知，定义域为(-∞，+∞)，求导数得

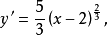
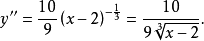
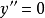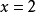由二阶导数可知，无 的点；当 时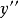， 不存在．见表2。

|| || 表2

由表2知，曲线的凹区间为（2，+∞），凸区间为（－∞，2）；拐点为（2，0）。2