[科普中国]-偶置换

偶置换是置换的一个子类，长度为2的轮换称为对换，每个置换都可以表示成对换的乘积。一个可以表示成偶数个对换的乘积称为偶置换。

简介当把置换写成对换的乘积时，不要求（也不能要求）这些对换没有公共的点，也不能保证表示的唯一性；甚至不能保证乘积中出现的对换的个数的唯一性。但是我们可以证明，当把一个置换 g 表示成对换的乘积，所需要的对换的个数的奇偶是被 g 完全确定的。一个可以表示成偶数个对换的乘积称为偶置换（even permutation），否则称为奇置换（odd permutation）。

性质两个偶置换的乘积，两个奇置换的乘积都是偶置换。

一个偶置换和一个奇置换乘起来是奇置换。

若 |Ω|=n，则在Ω 的全体置换中，有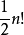个偶置换，有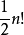奇置换。

全体偶置换在置换的乘法下成为一个群，称为Ω 上的交错群（alternating group），记作 Alt (Ω)。Alt (Ω) 是 Sym(Ω) 的正规子群。若 |Ω|=|Ω1|，Sym(n) 或 Sn来表示 n 元集合上的对称群。同样用 Alt(n)，或 An来表示 n 元集合上的交错群。交错群在有限群理论中具有重要地位。当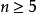时，An是单群。

置换群[permutation group]

置换群是由置换组成的群。一个有限集合到自身的双射称为置换（permutation）。设 Ω 为有限集合，其元素按惯例称为点。若α 为Ω 中一点，g 为Ω 一个置换，通常把α 在 g 下的像记作αg。设Ω={1,2,...,n}，则 Ω 的置换可表成

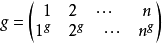的形状，这里把每个点的像写在点的下方。

例如，Ω={1,2,3,4,5}，

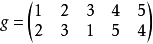就表示这样一个置换，它把 1 映成 2，把 2 映成 3，把 3 映成 1，把 4 和 5 互换。此时我们也把 g 写作 g=(123)(45) 的形状。

一般地，Ω={1,2,...,n} 上的任何置换都可以写成

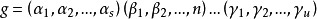的形状，这里 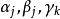都是Ω 的点，而且Ω 的每个点在右端恰好出现一次。上面的写法表示，g 把α1 映成α2，把α2 映成α3,...,又把α3 映成α1。同样，g 把β1 映成β2 ，把β2 映成β3,..., 又把βt 映成β1，等等。此处的 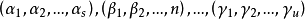都称为 轮换 (cycle)，s,t,...,u 称为它们的长度（length）。这种表示称为置换的轮换分解（eycle decomposition）。在此分解中出现的各轮换的长度之和为Ω 的长度 n。按照上面的方法，(123)(45) 也可写成(231)(54)，或(312)(45)，或(45)(231)等。这就是说，在轮换的分解中，各轮换的次序可以改变，同时轮换 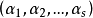也可用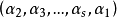 代替。我们还规定，在用轮换分解来表示置换时，长度为 1 的轮换可以省略。

若Ω 有 n 个点，则Ω 点置换共有 n！个。设 g，h 为两个置换，它们作为映射可用相乘，把乘积记住 gh，点α 在 gh 下的像为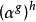。Ω 的全体置换在上述乘法下成为一个群，它称为Ω 上的对称群（symmetric group)，通常记住 Sym(Ω)。Sym(Ω)的任意子群称为Ω 上的置换群。

长度为 2 度轮换称为对换（transposition)。任何一个长度 2 的轮换可以写成对换可以写成对换的乘积。实际上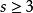，，有

。

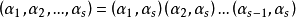进而每个置换都可以写成对换的乘积。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学