[科普中国]-自正交拉丁方

基本介绍

自正交拉丁方(self-orthogonal Latin square)是一类特殊的拉丁方，指与自身的转置相正交的拉丁方，亦即(2，1，3)共轭正交拉丁方。v阶自正交拉丁方存在的充分必要条件是v≠2，3，6。自正交拉丁方可用来安排一种特殊形式的网球赛，即所谓配偶回避的混合双打循环赛，设n对夫妇进行一场混合双打循环赛，要求：

1.配偶不出现在同一局比赛中，不论是作为伴对还是作为抗对；

2.性别相同的两个参赛者将作为抗对恰在一局中相遇；

3.每一对非配偶的异性参赛者将作为伴对在一局比赛中相遇，且作为抗对在又一局比赛中相遇。

这类安排对应于一个拉丁方A=(aij)。设第i对夫妇为i先生及i太太，当i先生与j先生在某一局中相遇时，与i先生搭档者设为aij太太，与j先生搭档者设为aji太太。于是，由上述安排得到的幂等拉丁方是自正交的，反之，由一个幂等自正交拉丁方可得到相应的循环赛安排，这样，配偶回避的混合双打循环赛安排等价于一个幂等自正交拉丁方，而后者的存在性又等价于自正交拉丁方的存在性1。

共轭正交拉丁方共轭正交拉丁方(conjugate orthogonal Latin squares)是一类特殊的拉丁方，若(Q，⊙)为一拟群，则在集Q上可定义5个新的二元运算⊙(i，j，k)如下：当a⊙b=c时，a⊙(1，3，2)c=b，b⊙(2，1，3)a=c，b⊙(2，3，1)c=a，c⊙(3，1，2)a=b，c⊙(3，2，1)b=a，由此得5个拟群(Q，⊙(i，j，k))，称为拟群(Q，⊙)的(i，j，k)共轭拟群，若拟群(Q，⊙)的乘法表所定义的拉丁方为L，则其(i，j，k)共轭拟群的乘法表所定义的拉丁方称为L的(i，j，k)共轭拉丁方，若拉丁方L与它的(i，j，k)共轭拉丁方正交，则称L为(i，j，k)共轭正交拉丁方，简记为(i，j，k)-COLS(v)，其中v为阶数。一个(2，1，3)共轭正交拉丁方通常称为自正交拉丁方。(3，2，1)-COLS(v)的存在性等价于(1，3，2)-COLS(v)的存在性，(3，1，2)-COLS(v)与(2，3，1)-COLS(v)也是同时存在或同时不存在的。共轭正交拉丁方的存在性问题已经解决，当且仅当v≠2，3，6时，存在(2，1，3)-COLS(v)，当且仅当v≠2，6时，存在(3，1，2)-COLS(v)及(3，2，1)-COLS(v)1。

相关性质定理一个拉丁方如若与其转置阵正交，则称为自正交拉丁方(self-orthogonalLatinsquare)。n阶自正交拉方记作SOLS(n)，下面主要关于自正交拉丁方的构作方法（详细证明过程可参考相应书籍）2。

定义1设A= (aij)为加法群Zn上的SOLS(n)，若对任意 都有

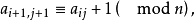则称A为一个循环SOLS(n)。

引理1 循环SOLS(12)与循环SOLS(15)都存在。

**证：**对n= 12,15,我们给出循环SOLS(n)的初始行如下:

(i)n=12，初始行: (1 8 3 6 2 9 11 1 10 5 7 4)；

(i)n=15，初始行: (0 2 11 6 10 13 5 14 4 7 12 1 9 8 3)。

下面是关于N.S.Mendelsohn关于自正交拉丁方的直接构作法。

定理1若(n,6)= 1，则存在循环SOLS(n)。

定理2 设q为素数幂，q≥4，则存在SOLS(q)。

引理2 若A是自正交拉丁方，则A的主对角线是截线2。

下面关于自正交拉丁方的递归构造方法，令

S= {n|存在SOLS(n)}.

定理3S是一个PBD闭集。

证明： 要证S是PBD闭集，也就是要证下述结论: 若存在B(K,1;v)使对任意k∈K都有SOLS(k)存在，则SOLS(v)也必存在。

设(X,A)为一个B(K,1;v).设B∈A,|B|=k∈K，可在B上构作一个SOLS (k)。由引理1，每一个自正交拉丁方的主对角线都是截线。因此经对B中元素作适当置换后，总可设所得到的SOLS(k)是幂等的，从而在由此所得到的正交阵列OA(k,1;4)中，对每一个元素a∈B,(a,a,a,a)T都是此OA(k,1;4)中的一列，将所有k个这样的列去掉，剩下的4x(k2-k)阵列记作DB。对每一个B∈A，都得到一个DB，将所有这些DB排成一行，再添上每个a∈X得到的列(a,a,a,a)T，由此得到一个阵列D，则D是个OA(v,1;4)，且由D的第3行与第4行得到的两个v阶拉丁方互为转置，由此即得到一个SOLS(v)，即v∈S，从而S为PBD闭集。

引理3设n= 10或14，则SOLS(n)存在。

引理4设n∈{18,26,30}，则SOLS(n)存在。

引理5 设n∈{38,42}，则SOLS(n)存在。

引理6设N(m) > 3，0≤t≤m，若SOLS(m)与SOLS(t)都存在，则SOLS(4m+t)也存在。

有了以上准备，现在可以给出自正交拉丁方存在性问题的完整解决，即证明下述著名的Brayton-Coppersmith-Hoffman (BCH)定理。

定理4设n为正整数，则SOLS(n)存在的充分必要条件为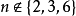 2。