[科普中国]-李型单群

概念介绍

李型单群(simple group of Lie type)是一类重要的特殊单群。谢瓦莱单群和单扭群统称为李型单群。任意域上的李型单群是按复数域上的单李群仿造出来的。复单李群对应于复单李代数。由于存在谢瓦莱基，复单李代数可以改造成为任意域上的李代数，谢瓦莱群就被定义为这个李代数的自同构群的某个子群。由李代数的邓金图的非平凡对称可以得到相应的谢瓦莱群的自同构，扭群就是在这个自同构下不变的某些元素所生成的群。有限域上的李型单群组成了最主要的有限单群系列。2

群群是一种只有一个运算的、比较简单的代数结构；是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。

单群单群是一类重要的群。即不含非平凡正规子群的群。若群G≠{e}，且除{e}及G本身外不再含其他的正规子群，则称G为单群。若此时G还是有限群，则称G为有限单群。有限单群的例子有：素数阶群，交错群An，n≥5。有限单群的研究是有限群论中一个十分活跃的领域。3

单李群单李群是与单李代数相应的李群。设G为连通李群，若它的李代数为单李代数，则G称为单李群。若G为单李群，且G1为G之真正规李子群，则G1为G之中心中离散子群。特别地，单李群之中心由有限或可数个元素构成。若G为半单李群，则G有单正规子群G1，G2，…，Gs，使得Gi为闭子群，且G=G1G2…Gs为半直乘积，即Gi∩GjC(G)，且Gi中元素和Gj中元素可交换。于是，半单李群的结构问题化为单李群的结构问题。

谢瓦莱群谢瓦莱群是与一类特殊李代数密切相关的群。设L是复数域上单李代数，Π是L的基础根系，Φ是L的根系，

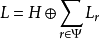是L的嘉当分解。根据谢瓦莱基定理，可以取嘉当子代数的基{hα|α∈Π}及每个根子空间Lr的基er，使L关于基{hα，er|α∈Π，r∈Φ}的乘法常数全是有理整数.这组基的整系数线性组合的全体LZ，按L的李乘法构成有理整数环Z上一个李代数.对任意域K，可将加群LK=KLZ定义成一个李代数，使[1Kx，1Ky]=1K[x，y].对任意r∈Φ与t∈K，ad(ter)：x→[ter，x]是LK的幂零微分，

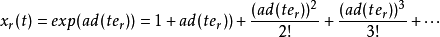是LK的自同构。所有的xr(t)(r∈Φ，t∈K)生成的群L(K)是LK的自同构群的一个子群，称为K上的谢瓦莱群。每个xr(t)(t∈Φ，t∈K) 称为L(K)的根元素，而Xr={xr(t)|t∈K}称为L(K)的根子群。当L分别是Al(l≥1)，Bl(l≥2)，Cl(l≥3)，Dl(l≥4)，El(6≤l≤8)，F4，G2型李代数时，分别得到谢瓦莱群Al(K)，Bl(K)，Cl(K)，Dl(K)，El(K)，F4(K)，G2(K)。其中Al(K)，Bl(K)，Cl(K)，Dl(K)分别同构于典型群PSLl+1(K)，PΩ2l+1(K，QB)(QB的指数=l)，PSp2l(K)，PΩ2l(K，QD)(QD的指数=l)。当K是q元有限域时，也将L(K)简记为L(q)。除A1(2)，A1(3)，B2(2)，G2(2)外，谢瓦莱群都是单群。4

扭群扭群是谢瓦莱群的重要子群。设单李代数L=Al，Dl，E6，B2，G2或F4，它的邓金图有非平凡的对称ρ，ρ的阶n=2或3.设K是域，且当L=B2或F4时K是特征2的完全域;当L=G2时K是特征3的完全域.若G=L(K)是K上L型谢瓦莱群，则存在G的自同构g，称为图自同构，将每个基础根α∈Π对应的根子群Xα变为基础根ρ(α)对应的根子群Xρ(α).域K的每个自同构τ也决定G的一个自同构，称为域自同构并仍记为τ，将每个根元素xr(t)变为xr(t).图自同构g与每个域自同构τ相交换，它们的乘积σ=gτ仍是G的自同构.选取非平凡的域自同构τ使σ=gτ与ρ具有相同的阶n，即σ=1.所有的正根r∈Φ对应的根子群Xr生成G的子群U，所有的负根r∈Φ对应的根子群Xr生成子群V.又，若

U={x∈U|σ(x)=x}，

V={x∈V|σ(x)=x}，

则U与V生成的子群记为L(K)，称为扭群。当n=2时，L(K)称为K上L型扭群，包括Al(K)，Dl(K)，E(K)，B2(K)，G2(K)，F4(K)；当n=3时，L(K)为D4(K)，称为K上D4型三次扭群.群B2(K)又称为铃木群；群G2(K)，F4(K)又称为雷群.群Al(K)同构于酉群PSUl+1(K，f)，f的指数为(l+1)/2(当l奇)或l/2(当l偶).群Dl(K)同构于正交群PΩ2l(K0，Q)，其中K0是域自同构L的不变子域，Q的指数为l-1.当K是q元域时可将L(K)简记为L(q).除A2(2)，B2(2)，G2(3)，F4(2)外，扭群都是单群。5