[科普中国]-亚阿贝尔群

概念介绍

亚阿贝尔群(metAbelian group)是一种可解群。指导出列长度至多为2的群。设G是群，若G有导出列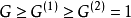，则称G为亚阿贝尔群。设G是群，若G有循环的正规子群N，使得G/N为循环群，则称G为亚循环群。亚循环群是特殊的超可解群。1

群

群是一种只有一个运算的、比较简单的代数结构；是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：2

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。

可解群

一种重要的群类.即可由交换群经有限步叠加而得的群。若群G有一个有限长的正规群列G≥G1≥G2≥…≥Gn=1，使得每个商因子都是交换群，则称G是一个可解群，或称G是可解的。可解群的概念源自伽罗瓦(Galois，E.)对解代数方程的研究，他发现由一个代数方程的所有解可产生一个置换群(也就是扩域的自同构群，称之为一个伽罗瓦群)，这个代数方程能用根式解出当且仅当该群具有正规列。可解群的名称由此而来.霍尔(Hall，P.)于20世纪30—40年代对有限可解群理论做了奠基性贡献。费特-汤普森奇阶定理成为另一个里程碑。近几十年，有限可解群研究仍属活跃领域。例如群系等群类理论就始于有限可解群研究并以可解群为重点。对无限可解群的研究也有了长足的进步。尽管有限可解群的研究方法与成果不能完全推到无限可解群，但带交换商因子的正规列这一定义条件使很多思想与工具，如模论、表示论等，均可发挥出色的作用。

超可解群

超可解群是一种重要的群类。指能用循环群有限叠加起来的群。若一个群有一个有限长的正规列且其商因子均为循环群，则称之为超可解群。有限超可解群也就是秩为1的有限可解群。对超可解群的研究已经形成了相当丰富的理论。对有限超可解群的研究已很透彻，贝尔(Baer，R.)、胡佩特(Huppert，B.)等人有重要贡献。对无限超可解群也有丰富的研究成果。

阿贝尔群

阿贝尔群亦称交换群。一种重要的群类。对于群G中任意二元a，b，一般地，ab≠ba。若群G的运算满足交换律，即对任意的a，b∈G都有ab=ba，则称G为阿贝尔群。由于阿贝尔(Abel，N.H.)首先研究了交换群，所以通常称这类群为阿贝尔群。交换群的运算常用加法来表示，此时群的单位元用0(零元)表示，a的逆元记为-a(称为a的负元).用加法表示的交换群称为加法群或加群。3

循环群

循环群是一种重要的群。即由一个元素生成的群。循环群分为两类：一类是有限循环群，n个元的有限循环群与模n的剩余类加群同构；另一类是无限循环群，它与整数加法群同构.循环群是特殊的阿贝尔群。循环群的子群和商群仍是循环群。

一个群G，其中存在一个元素a，使得G中任何元素都可以表示成ak的形式(k为整数)。a称为它的生成元。循环群是一种交换群。

循环群也叫有限单演群。

例如，单位1的全体n次根的集合，即是说赋以乘法的方程zn=1的全体复数根的集合是n阶循环群。赋以加法的集合Z/nZ是n阶循环群。4

人物简介

阿贝尔是一位伟大的挪威数学家。生于芬岛，卒于弗鲁兰。阿贝尔的父亲是一位基督教牧师，家境贫困。13岁时阿贝尔入奥斯陆一所教会学校学习，15岁时幸遇优秀数学教师霍尔姆伯。他发现了阿贝尔的数学天才并给予悉心指导。阿贝尔一生得到霍尔姆伯许多帮助。1821年，在霍尔姆伯等人的资助下，阿贝尔进入克里斯蒂安尼亚大学学习。1824年，他解决了困扰数学界200多年的五次方程求解问题，证明了一般五次方程不可能用根式求解，开辟了研究近世代数方程论的道路。他的论文以小册子的形式刊行，也送给了高斯，但没有引起任何反响。1825年阿贝尔到欧洲大陆，准备继续深造并谋求职务。在德国他结识了克雷尔，这是在他一生中第二个对他的事业有极大帮助的人。他与施泰纳建议克雷尔创办了著名数学刊物《纯粹与应用数学杂志》。这个杂志头三卷发表了阿贝尔的22篇包括方程论(见《高于四次的一般方程的代数求解之不可能性的证明》)、无穷级数、椭圆函数论等方面的论文。阿贝尔在欧洲大陆没有谋到合适的职位，1827年他贫病交迫地回到了挪威。一年以后，不到27岁的阿贝尔就病逝了。他去世的第二天，克雷尔来信通知他被柏林大学任命为教授。阿贝尔对数学的贡献是多方面的。除了五次方程以外，他还研究了更广一类的代数方程，后人发现这是具有交换的伽罗瓦群的方程。为了纪念他，人们称交换群为阿贝尔群。阿贝尔还是公认的椭圆函数论的奠基人之一。他发现了椭圆函数的加法定理、双周期性，并引进椭圆积分的反演。他的一系列工作为椭圆函数论的研究开拓了道路。他还研究无穷级数，得到一些判别准则以及关于幂级数求和的定理。这些工作使他成为分析学严格化的推动者。5