自由半群
自由半群是指不附加任何其他条件的半群。若X是一非空集合,做:
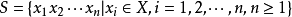 则S用如下定义的运算做成一个半群:
则S用如下定义的运算做成一个半群:
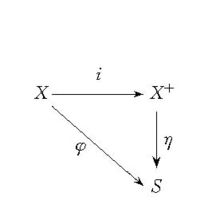
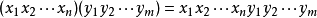 称S是X上的自由半群,常记S=X.记(X)=X,称X为X上的自由幺半群。自由半群无任何幂等元,因此是无任何正则元的半群。它有如下的特征:设X是一集合,关于任意半群S和X到S的任意映射φ,存在X到S的惟一的同态η使得下图交换(即ηi=φ),其中,i为X到X的包含映射。反之,若用半群T和映射j:X→T分别代替上面的X和i:X→X使上事实成立,则T同构于X。自由幺半群也有类似的特征。2
称S是X上的自由半群,常记S=X.记(X)=X,称X为X上的自由幺半群。自由半群无任何幂等元,因此是无任何正则元的半群。它有如下的特征:设X是一集合,关于任意半群S和X到S的任意映射φ,存在X到S的惟一的同态η使得下图交换(即ηi=φ),其中,i为X到X的包含映射。反之,若用半群T和映射j:X→T分别代替上面的X和i:X→X使上事实成立,则T同构于X。自由幺半群也有类似的特征。2
自由群设S为任意集合,S中有限个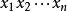 连在一起叫做是一个字。字
连在一起叫做是一个字。字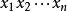 和
和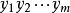 相等,如果n=m且
相等,如果n=m且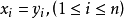 。以
。以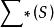 表示所有这样的字(包含空字1)组成的集合。
表示所有这样的字(包含空字1)组成的集合。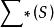 中定义两个字的运算为,
中定义两个字的运算为,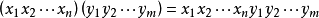 ,且对每个字
,且对每个字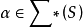 ,规定
,规定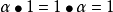 ,则这个运算显然满足结合律,所以
,则这个运算显然满足结合律,所以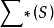 对上述运算形成一个含幺半群,它称为集合S上的自由含幺半群,集合叫做
对上述运算形成一个含幺半群,它称为集合S上的自由含幺半群,集合叫做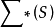 的基。“自由”一词意味着
的基。“自由”一词意味着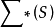 中除了含幺半群定义中的要求之外,没有任何其他约束条件。
中除了含幺半群定义中的要求之外,没有任何其他约束条件。
如果将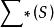 自由含幺半群扩大成群,每个元素
自由含幺半群扩大成群,每个元素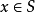 应当有逆元素,所以给了集合S之后,再考虑集合
应当有逆元素,所以给了集合S之后,再考虑集合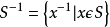 。令
。令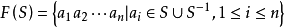 ,这里当n=0时,规定
,这里当n=0时,规定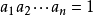 。
。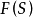 中运算仍定义
中运算仍定义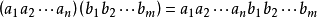 ,但是约定
,但是约定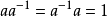 ,对每个
,对每个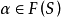 ,
,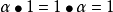 。这样,
。这样,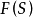 中每个元素均有逆元素,例如的逆元素
中每个元素均有逆元素,例如的逆元素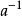 为
为 。
。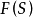 对于上述运算及约定构成群,叫做集合S上的自由群,S叫做此自由群的基。显然S是群
对于上述运算及约定构成群,叫做集合S上的自由群,S叫做此自由群的基。显然S是群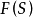 的一个生成元系。如果S是有限集,则
的一个生成元系。如果S是有限集,则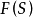 叫做有限生成自由群。特别当
叫做有限生成自由群。特别当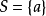 时,就
时,就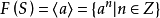 是无限循环群,而当时
是无限循环群,而当时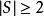 ,
,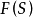 是无限非阿贝尔群。
是无限非阿贝尔群。
群群是一种只有一个运算的、比较简单的代数结构;是可用来建立许多其他代数系统的一种基本结构。
设G为一个非空集合,a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”,运算结果称为“乘积”)满足:
(1)封闭性,a·b∈G;
(2)结合律,即(a·b)c = a·(b·c);
(3)对G中任意元素a、b,在G中存在惟一的元素x,y,使得a·x= b,y·a=b,则称G对于所定义的运算“·”构成一个群。例如,所有不等于零的实数,关于通常的乘法构成一个群;时针转动(关于模12加法),构成一个群。
满足交换律的群,称为交换群。
群是数学最重要的概念之一,已渗透到现代数学的所有分支及其他学科中。凡是涉及对称,就存在群。例如,可以用研究图形在变换群下保持不变的性质,来定义各种几何学,即利用变换群对几何学进行分类。可以说,不了解群,就不可能理解现代数学。
1770年,拉格朗日在讨论代数方程根之间的置换时,首先引入群的概念,而它的名称,是伽罗华在1830年首先提出的。
半群半群是最简单、最自然的一类代数系统。一个非空集合S连同定义在它上面的一个结合的(即满足结合律的)二元运算“·”的代数系统(S,·)称为一个半群。半群(S,·)简记为S。
半群是群的推广。群自然是半群;反之显然未必。半群也是环的推广。环在只考虑它的乘法运算的时候是一个半群,称为环的乘半群;但任何一个带零半群却未必是某个环的乘半群。半群代数理论的系统研究始于20世纪50年代(虽然,这方面的工作可追溯到1904年苏士凯维奇(Suschkwitz,A.K.)关于有限半群的论文).在数学内部和外部的巨大推动下,半群理论已成为代数学的一个公认的分支学科,并早已以其特有的方法独立于群论和环论之外.在20世纪60年代,苏联和美国率先出版了两本专著,利雅平(Ляпин,E.C.)的《半群》和克利福德(Clifford,A.H.)与普雷斯顿(Preston,G.B.)的两卷《半群代数理论》,这对半群代数理论的发展,在国际上起了巨大的推动作用.由德国斯普林格出版社出版的《半群论坛》更是有关半群理论的一个重要的国际性专门刊物.许多数学家在世界各地开展半群理论的研究和各层次高级人才的培养(直到博士后).半群代数理论是半群理论中最基本、最活跃、也最富成果的一部分.此外,尚有半群的分析、拓扑和序理论。3
阿贝尔群阿贝尔群亦称交换群。一种重要的群类。对于群G中任意二元a,b,一般地,ab≠ba。若群G的运算满足交换律,即对任意的a,b∈G都有ab=ba,则称G为阿贝尔群。由于阿贝尔(Abel,N.H.)首先研究了交换群,所以通常称这类群为阿贝尔群。交换群的运算常用加法来表示,此时群的单位元用0(零元)表示,a的逆元记为-a(称为a的负元)。用加法表示的交换群称为加法群或加群。
设G是一个群,如果对任何a,b∈G,ab=ba,则称G是一个交换群,或阿贝尔群。阿贝尔群的子群都是正规的。在阿贝尔群中,我们把运算记为加法。设G是一个群,S是G的一个子集,G的包含S的所有子群的交称为G的由S生成的子群,记作〈S〉。如果G=〈S〉,则称G是由S生成的,S是G的一个生成元集。如果G有一个有限生成子集,则称G是有限生成的。设G是一个群,A,B是G的子群,如果G=〈A∪B〉,A∩B仅含G的单位元,则称G是子群A,B的直积,当G是阿贝尔群时,也称G是子群A,B的直和,记作G=A⊕B。循环群是阿贝尔群。4




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国