若G是局部紧致阿贝尔群,G的特征标是一个从G到圆群T的连续群同态;特征标在逐点乘法下构成一个群,一个特征标的逆元是它的复共轭。可证明所有G上的特征标在紧致开拓扑(即:以紧集上的一致收敛定义收敛性)下构成一个局部紧致阿贝尔群,称作对偶群。
定义若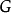 是局部紧致阿贝尔群,
是局部紧致阿贝尔群,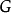 的特征标是一个从
的特征标是一个从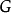 到圆群
到圆群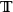 的连续群同态;特征标在逐点乘法下构成一个群,一个特征标的逆元是它的复共轭。可证明所有
的连续群同态;特征标在逐点乘法下构成一个群,一个特征标的逆元是它的复共轭。可证明所有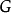 上的特征标在紧致开拓扑(即:以紧集上的一致收敛定义收敛性)下构成一个局部紧致阿贝尔群,称作对偶群,记为
上的特征标在紧致开拓扑(即:以紧集上的一致收敛定义收敛性)下构成一个局部紧致阿贝尔群,称作对偶群,记为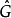 或
或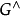 。若
。若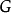 可分,则
可分,则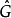 可度量化,对一般的
可度量化,对一般的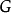 则不尽然。
则不尽然。
这可用线性代数中的对偶空间来类比,就像一个布于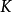 的向量空间
的向量空间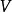 有对偶空间
有对偶空间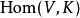 ,对偶群可看成
,对偶群可看成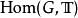 。更抽象的说,这两者都是可表函子,被
。更抽象的说,这两者都是可表函子,被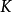 及
及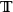 所表示。
所表示。
定理:二次对偶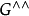 与
与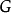 有个自然同构。
有个自然同构。
在此,“自然”或“典范”同构意谓一个“自然地”定义的映射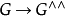 ,要点是它在范畴中满足函子性(详见条目范畴论)。举例明之:任何有限阿贝尔群都同构于其对偶群,但并不存在典范同构1。
,要点是它在范畴中满足函子性(详见条目范畴论)。举例明之:任何有限阿贝尔群都同构于其对偶群,但并不存在典范同构1。
定理中的自然同构定义如下:
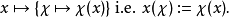
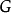 换言之,我们借着将一个元素
换言之,我们借着将一个元素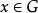 在每个的特征上求值,得到一个
在每个的特征上求值,得到一个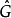 上的特征。
上的特征。
例子在整数对加法形成的无穷循环群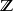 (配上离散拓扑)上,设
(配上离散拓扑)上,设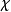 为一特征,则
为一特征,则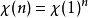 ,因此
,因此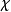 决定于
决定于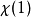 的值;反之,给定一个,必存在特征
的值;反之,给定一个,必存在特征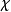 使得
使得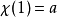 ,由此得到群同构群同构
,由此得到群同构群同构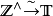 。此外也容易验证
。此外也容易验证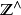 上的紧-开拓扑对应到
上的紧-开拓扑对应到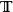 诱导自
诱导自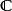 的拓扑。
的拓扑。
因此,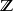 的对偶群自然地同构于
的对偶群自然地同构于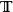 。
。
反之,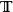 上的特征皆形如
上的特征皆形如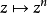 ,其中n是整数。由于
,其中n是整数。由于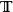 是紧的,其对偶群上的拓扑由一致收敛性给出,对应的不外是
是紧的,其对偶群上的拓扑由一致收敛性给出,对应的不外是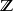 上的离散拓扑。因此
上的离散拓扑。因此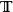 的对偶群自然地同构于
的对偶群自然地同构于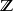 。
。
实数对加法构成的群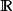 同构于自身的对偶群;
同构于自身的对偶群;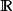 上的特征皆形如
上的特征皆形如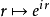 ,其中
,其中 是实数。借着这些对偶性,下节描述的傅里叶变换将符应于
是实数。借着这些对偶性,下节描述的傅里叶变换将符应于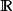 上的古典版本
上的古典版本
扩展对偶群与对偶函子:
函子的观点对于研究对偶群是很有用的。以下将以LCA表示所有局部紧阿贝尔群及其间的连续群同态构成之范畴。
对偶群的构造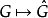 给出一个对偶函子
给出一个对偶函子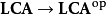 ,其二次迭代
,其二次迭代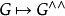 遂给出对偶函子:
遂给出对偶函子: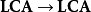 。
。
定理:对偶函子是一个范畴等价。
定理:对偶函子的二次迭代自然同构于LCA上的恒等函子2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国