简介
测地坐标系是曲面上的一种特殊坐标系。在曲面上取一族测地线为u曲线,取这族测地线的正交轨线为二曲线(称为测地平行线),这种坐标系称为测地坐标系。例,平面极坐标系,一族坐标曲线是由极点出发的射线,这是平面上的测地线,另一族坐标曲线是以极点为中心的同心圆,它们是上述测地线的正交轨线,因此平面极坐标系是一种测地坐标系。
测地坐标系分成测地平行坐标系和测地极坐标系两种。测地坐标是在曲面内蕴几何学意义下最简单、最适当的坐标系。
建立方法测地平行坐标构作如下:
取一条测地线C₀作为u=0曲线;经过曲线C₀上每一点、沿着C₀正交的方向作测地线,得到依赖一个参数的测地线族作为u曲线族;再作上述测地线族的正交轨线,作为v曲线族。此时,曲面的第一基本型成为
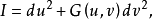
其中函数G(u,v)满足条件
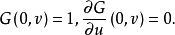
测地平行坐标系中曲线C0点附近是成立的。
测地极坐标系的构作如下:
取一点p,从点p出发沿各个切方向作测地射线,得到依赖一个参数的测地射线族,作为u曲线族;再作以点p为中心点测地圆(geodesic circle),即到点p的距离为常数的点点轨迹,作为v曲线族。此时,这两族曲线是彼此正交的,故曲面的第一基本型成为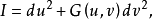 其中函数G(u,v)满足条件
其中函数G(u,v)满足条件
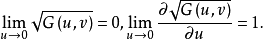
测地极坐标系在点p的附近、除去从点p出发点一条测地射线以外的区域上是成立的。2
测地线曲面上测地曲率恒为零的曲线称为该曲面上的测地线,测地线所满足的微分方程是
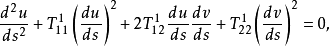
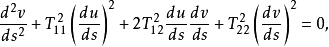
或者写成一般的形式
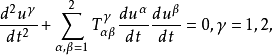 式中,
式中,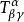 是曲面的克氏符号,
是曲面的克氏符号,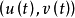 (也记成
(也记成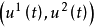 )是测地线的参数方程。当曲面作保长变换时,测地线变成测地线。因此,测地线是属于曲面的内蕴几何概念。当曲面上取正交参数曲线网时,测地线的微分方程成为
)是测地线的参数方程。当曲面作保长变换时,测地线变成测地线。因此,测地线是属于曲面的内蕴几何概念。当曲面上取正交参数曲线网时,测地线的微分方程成为
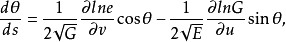
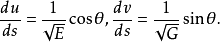




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国