定义
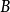 设
设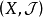 是拓扑空间,
是拓扑空间,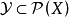 ,若
,若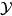 中元素的一切有限交之族,即
中元素的一切有限交之族,即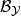 ={
={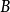
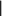 是
是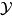 中有限个元素的交}是集合X上的拓扑
中有限个元素的交}是集合X上的拓扑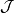 的基,则称
的基,则称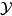 是拓扑
是拓扑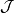 的子基,
的子基,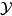 中的元素称为子基开集。2
中的元素称为子基开集。2
相关概念设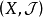 是拓扑空间,
是拓扑空间,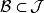 ,若
,若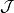 的元素都可表示为
的元素都可表示为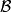 中某些元素的并,即对于
中某些元素的并,即对于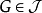 ,存在
,存在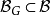 使得
使得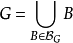 ,则称
,则称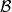 是拓扑
是拓扑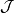 的基或拓扑基,也称为拓扑空间
的基或拓扑基,也称为拓扑空间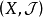 的基或拓扑基,
的基或拓扑基,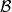 中的元素称为基开集。2
中的元素称为基开集。2
例1 设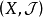 是任意拓扑空间,则
是任意拓扑空间,则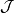 就是它的基。
就是它的基。
例2 设X是非空集,记
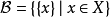 则
则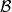 是集合X上的离散拓扑的基。
是集合X上的离散拓扑的基。
相关定理定理1设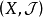 是拓扑空间,
是拓扑空间,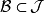 ,则
,则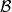 是拓扑
是拓扑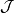 的基的充分必要条件是对于任意
的基的充分必要条件是对于任意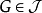 ,任意
,任意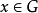 ,存在
,存在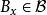 ,使得
,使得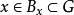 。2
。2
证明: 必要性:对于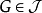 ,因为
,因为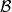 是
是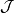 的基,从而
的基,从而
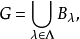 其中
其中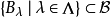 ,所以对于任意
,所以对于任意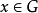 ,存在
,存在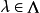 ,使得
,使得
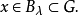 充分性:任取
充分性:任取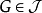 ,若
,若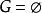 ,则取
,则取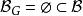 ,从而
,从而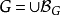 ,若
,若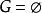 ,则对于任意
,则对于任意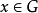 ,存在
,存在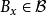 使得
使得
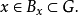 于是
于是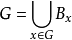 ,记
,记 ,因此
,因此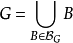 ,又
,又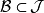 ,所以
,所以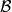 是
是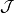 的基。
的基。
定理2设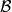 是非空集X的一个子集族,则
是非空集X的一个子集族,则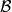 是集合X 上的某一拓扑的基的充分必要条件是
是集合X 上的某一拓扑的基的充分必要条件是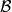 满足下列条件
满足下列条件
(1)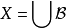 ;
;
(2)对于任意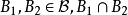 是
是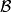 中某些元素的并。
中某些元素的并。
若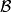 满足上述两个条件,则集合X上以
满足上述两个条件,则集合X上以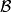 为基的拓扑是唯一的,此拓扑称为以
为基的拓扑是唯一的,此拓扑称为以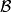 为基生成的集合X上的拓扑。
为基生成的集合X上的拓扑。
定理3设X为非空集,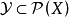 ,并且
,并且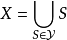 ,则集合X上存在唯一拓扑以
,则集合X上存在唯一拓扑以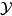 为子基,这个拓扑称为以
为子基,这个拓扑称为以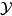 为子基生成的集合X上的拓扑2。
为子基生成的集合X上的拓扑2。
证明 记
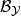 ={B
={B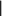 B是
B是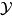 中有限个元素的交}.
中有限个元素的交}.
因为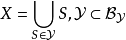 ,从而
,从而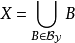 ,又对于
,又对于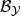 中任意两个元素的交是
中任意两个元素的交是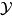 中元素的有限交,可见
中元素的有限交,可见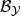 的任意两个元素的交属于
的任意两个元素的交属于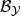 ,于是这个交是
,于是这个交是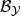 中元素的并。因此,从定理2中条件的充分性可知,集合X上有拓扑
中元素的并。因此,从定理2中条件的充分性可知,集合X上有拓扑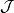 以
以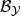 为它的基,所以
为它的基,所以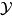 是此拓扑
是此拓扑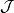 的子基,若
的子基,若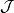 *是以
*是以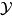 为子基的集合X上的另一拓扑,则根据子基定义,
为子基的集合X上的另一拓扑,则根据子基定义,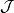 *是以
*是以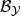 为基,所以,由定理2可知
为基,所以,由定理2可知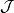 *=
*=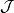 。 2
。 2
例3 设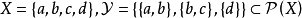 ,则以
,则以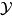 为子基生成的集合X上的拓扑是
为子基生成的集合X上的拓扑是




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国