域上代数相关集(algebraically dependent setover a field)是与超越基密切相关的一个概念。设K是F的域扩张,S是K的子集。若y∈K是F(S)上的代数元,则称y在F上与S是代数相关的;否则,称为代数无关的。
概念域上代数相关集(algebraically dependent setover a field)是与超越基密切相关的一个概念。设K是F的域扩张,S是K的子集。若y∈K是F(S)上的代数元,则称y在F上与S是代数相关的;否则,称为代数无关的。任何子集SK,若有某个x∈S,它与S\{x}在F上代数相关,则称S是F上(或者关于F)的一个代数相关集;否则,为F上的一个代数无关集(通常又称为超越集)。当S={x}时,{x}成为F上的代数相关集等价于x是F上的代数元;{x}是F上的超越集等价于x是F上的超越元。1
超越基超越基亦称极大超越集。域论的基本概念之一。它是线性代数中基概念的推广,是扩域的极大代数无关集。设K是域F的扩域,K的一个子集S称为K在F上的超越基,是指:S在F上代数无关,K是F(S)的代数扩域。域F的任一扩域K都存在超越基。超越基不是惟一的,但它的基数相等,称此基数为K在F上的超越次数,记为tr.degFK或tr.deg(K/F)。若L是F的扩域,K为中间域,则:
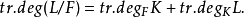 代数扩域的超越基为空集,它的超越次数规定为零。
代数扩域的超越基为空集,它的超越次数规定为零。
域论代数数论的重要理论之一。它深刻地刻画了(相对)阿贝尔扩张。基本定理如下:若K/k为数域的有限阿贝尔扩张,伽罗瓦群为G=G(K/k),则存在k的模f(称为K/k的导子,是k的一个除子),使得对k的任意的模m,由f|m得出G同构于m射线类群I(m)/PmN(m),式中I(m)为与m互素的k的理想集,N(m)为与m互素的K的理想到k的范全体,Pm为模m余1的α∈k生成的主理想集。且k的素除子v在K分歧当且仅当v|f;k的与m互素的素理想p在K完全分裂当且仅当p∈PmN(m)。反之,对k的任一模m及I(m)的任一含Pm子群H,总存在惟一阿贝尔扩张K/k,使得H=kPmN(m)且上述事实均成立。特别地,G(K/k)I(m)/H.更经常的是用伊代尔语言叙述类域论的定理。基本定理:若K/k为数域的有限阿贝尔扩张,则伽罗瓦群G(K/k)同构于Jk/kNJk,式中Jk为k的伊代尔群,NJK为K的伊代尔群到k的范。上述群的同构由阿廷映射给出。由此可得出,数域k的诸有限阿贝尔扩张K/k与Jk的含k诸开子群H之间一一对应,即K对应于H=kNJK,称为H的类域,G(K/k)Jk/H;这一对应是这两个格(对于复合(或积及交))的反向(包含关系)格同构。类域论有系统的定理和应用,有多种不同的表述方式。对于局部域的阿贝尔扩张有类似的定理(局部类域论),对于有限域上的单变量函数域也有类似的定理。
域的扩张域论的基本概念之一。若域K包含域F作为它的子域,则称K是F的一个扩张(或扩域),F称为基域,常记为K/F。此时,K可以看成F上的向量空间。研究扩域K(相对于基域F)的代数性质,是域论研究的一个基本内容。
若域E是F的扩域,K是E的扩域,则称E是域扩张K/F的中间域。若K/F是域扩张,S是K的子集,且F(S)是K的含F与S的最小子域,称F(S)为F添加S的扩域。当S={α1,α2,…,αn}是有限集合时,F(α1,α2,…,αn)称为添加α1,α2,…,αn于F的有限生成扩域(或者F上的有限生成扩张)。它由一切形如f(α1,α2,…,αn)/g(α1,α2,…,αn)的元组成,其中α1,α2,…,αn∈S,f,g是F上的n元多项式且g(α1,α2,…,αn)≠0。
由于这个原因,当F(α1,α2,…,αn)关于F的超越次数≥1时,F(α1,α2,…,αn)也称为F上的代数函数域.当S={α}时,称F(α)为F的单扩张域,也称本原扩域。F的有限代数扩域K是单扩域的充分必要条件是,扩域K与基域间存在有限个中间域。这是施泰尼茨(Steinitz,E.)证明的。1
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学





 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国