[科普中国]-实闭域

定义

实闭域的例子很多，最常见的是：实数域R；由所有实代数数所成的域RAlg。实闭域只有惟一的序>，它由a>0当且仅当a=b所确定，换言之，它的惟一的正锥是由所有平方元所组成。在实闭域上，任何一元多项式都能表为一次与二次不可约因式之积。实闭域与代数闭域间的紧密关系，可以从下面的事实认知：设Ω是一个代数闭域，F是它的真子域。若Ω/F是有限扩张，则F是实闭域，并且有Ω=F()。实闭域还有一个重要性质：任何一条初等的代数命题，若在某一个实闭域上成立，则必然在所有的实闭域上成立。这个结论被称为塔尔斯基(Tarski，A.)原则(或定理)。根据这个原则，凡在实数域R上成立的初等代数命题，在任何实闭域上也成立。

形式实域假设所论之域的特征数皆为零。若在一个域 中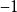， 无法写成平方和（表法： ），则称 是形式实的。

每个有序域都是形式实域；形式实的定义本身不涉及序结构，但借由实闭包的存在性可证明每个形式实域皆带序结构。

实封闭域一个实封闭域 若满足下列等价条件，则称之实封闭域：

上存在一个序结构，使得其中每个正元素皆可表为平方，且任何奇数次多项式都有根。

上存在一个序结构，使之满足中间值定理。

对任意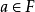 ，或者 或者 ；且任何奇数次多项式都有根。

非代数封闭，而 代数封闭。

若 ， 是形式实的，则 。

我们可以纯以代数性质定义实封闭域，并由 得到唯一的序结构1。

实闭包对任何形式实域 ，都存在代数扩张 ，使得 是实封闭的。我们称 是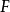 的一个实闭包。实闭包并不唯一。

若在 上固定一个序结构，并要求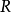 的序结构与之相容；则此时实闭包 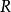存在并唯一，且 。

例子 实数域

；它是 的实闭包。

可计算数

Puiseux级数2

模型论观点实封闭域的研究首先由数学家展开，随后引起了逻辑学家的兴趣。采用形式语言 ，设 为实封闭域（带序结构）的 一阶理论，塔斯基证明了 上有量词消去；因此任两个 的模型都是初等等价的。一方面，我们可运用 上的特有工具（微积分、拓扑等等）证明一般实封闭域上的一阶句子；另一方面，则可透过适当的域扩张解决 上的问题，后一方向上最著名的成就是 Abraham Robinson 对希尔伯特第十七问题的证明。

如果改采形式语言 ，并取实封闭域的代数定义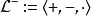 ，此时则无法消去量词（在 中考虑公式 ）。

设 是实封闭域，换言之 ，根据 上的量词消去， 上的可定义集只是有限多个线段与孤立点的并集。此性质称作O-极小性，它较量词消去为弱，却是研究 上可定义集的几何构造之关键。

量词消去也蕴含 的可判定性，然而塔斯基给出的算法其复杂度过高，并不实用。

若承认广义连续统假设，则可进一步以超积描述实封闭域的性状3。