[科普中国]-广义除数问题

广义除数问题(generalized divisor problem)是数论中的重要问题。数论是研究数的性质和规律的一门学科。是数学的一个重要分支。对于数学的许多分支学科(例如函数论、几何、代数、概率论、计算数学、组合数学等)以及应用学科(例如通信技术、密码学等)的发展有着深刻的影响。1

概念广义除数问题是数论中的重要问题。若dk(n)表示将n表为k个因子乘积的表法种数，又若：

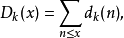则有：

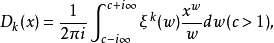其中ζ(w)为黎曼ζ函数，w=1为一k次极点，其上的留数形如xPk(log x)。此外，Pk为一k-1次多项式，记Dk(x)=xPk(logx)+Δk(x)。当k=2时，即为除数问题；当k>2时，即为广义除数问题。其定义αk为使Δk(x)=O(x)成立的数θ的下极限，估计αk即为广义除数问题的中心。对αk的上界估计，其结果有：

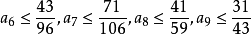等。一般地，αk≤(k-1)/(k+2)，k=4，5，…(哈代-李特尔伍德，1992年)，下界估计为αk≥(k-1)/2k(哈代(Hardy，G.H.)，1915年)，猜想结果是αk=(k-1)/2k。上列问题，至今仍未解决。2

数论研究数的性质和规律的一门学科。是数学的一个重要分支。对于数学的许多分支学科(例如函数论、几何、代数、概率论、计算数学、组合数学等)以及应用学科(例如通信技术、密码学等)的发展有着深刻的影响。其他学科的研究成果和思想方法，也对数论的发展有着重要的作用。数论按其内容和方法大致可分为初等的、解析的、代数的与几何的四类。

初等数论主要是用算术方法研究有理整数性质，包括整数的整除性、同余式、素数、原根、不定方程等，它不需要较为深入的分析和代数工具，是数学中古老的分支之一.远在公元前3世纪，古希腊数学家欧几里得(Euclid)就证明了素数的个数是无穷的.中国古代的《孙子算经》中给出了解一次同余式组的算法，即著名的“孙子定理”或称“中国剩余定理”.从17世纪到19世纪，法国数学家费马(Fermat，P.de)、瑞士数学家欧拉(Euler，L.)、法国数学家勒让德(Legendre，A.M.)、德国数学家高斯(Gauss，C.F.)等人的工作大大发展和丰富了初等数论的内容.另外，对初等数论中某些问题的研究，进一步发展了数学中的新分支.如对不定方程和高次互反律的研究，促进了代数数论和类域论的发展.近几十年来，初等数论在计算机科学、组合数学、密码学、信号的数字处理等领域得到广泛的应用，取得了许多深刻的结果.

解析数论在本质上是利用数学中的解析工具来研究数论问题，主要的方法有复积分法、圆法以及三角和方法.在素数分布问题的研究中，俄罗斯数学家切比雪夫(Чебышев，П.Л.)首先引进了与

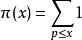密切相关的函数：

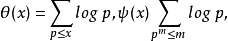并证明了θ(x)~x，ψ(x)~x都等价于素数定理，从而为素数定理的研究做出了重要贡献。德国数学家黎曼(Riemann，G.F.B.)首先对复变数s的函数：

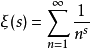做了系统和深刻的研究，对素数论与函数论的发展产生了深远的影响。由于英国数学家哈代(Hardy，G.H.)和李特尔伍德(Littlewood，J.E.)的强有力的方法——圆法，以及维诺格拉多夫(Виноградов，И.М.)所创造的“三角和方法”，使得关于奇数的哥德巴赫猜想获得了基本解决，并使华林问题关于G(k)的估计得到了极为深刻的结果。中国数学家华罗庚在三角和以及一系列著名数论问题中做出了举世公认的贡献。特别是陈景润关于偶数的哥德巴赫猜想的(1+2)的杰出成果，在国际数学界引起了强烈的反响。另外，塞尔贝格(Selberg，A.)、林尼克(Линник，Ю.В.)、邦别里(Bombieri，E.)以及中国数学家王元、潘承洞等在筛法、零点密度、均值定理等许多方面也做出了重要贡献。

代数数论最初的形成和发展，主要是由于对互反律和费马大定理等不定方程的研究所推动.目前，代数数论已成为数论中一个内容异常丰富的分支。代数数论研究的主要对象是代数数域，特别是研究一个给定的代数数域中代数整数的算术性质。代数数就是方程a0x+a1x+…+an-1x+an=0的根，其中a0，a1，…，an-1，an都是有理整数.非代数数就称为“超越数”，近年来关于超越数的深入研究已发展成为数论的一个独立的分支——超越数论。德国数学家库默尔(Kummer，E.E.)为了解决费马大定理，首先创立了理想数理论，为代数数论奠定了基础。德国数学家戴德金(Dedekind，J.W.R.)系统地发展了库默尔理论，建立了代数数论的基本理论，主要是代数数域的整数环的结构、素理想分解、单位群、理想类群性质等. 亨泽尔(Hensel，K.)开创的p-adic数理论，将赋值论和局部域的研究方法引入代数数论，并最终导致伊代尔和阿代尔概念的引入。19世纪末，由德国数学家希尔伯特(Hilbert，D.)开始，至1927年，由日本数学家高木贞治(Takagi，T.)和阿廷(Artin，E.)完成的类域论，是代数数论的最主要理论之一，它将扩域的伽罗瓦群与基域的理想类群(或伊代尔群)联系起来。目前，代数数论的研究手段和范围已大为扩展，包括代数、函数论、算术、代数几何等各种方法。希尔伯特、克罗内克(Kronecker，L.)在二次域理论，图埃(Thue，A.)、西格尔(Siegel，C.L.)、罗特(Roth，K.F.)在丢番图逼近论中以及外尔(Weyl，(C.H.)H.)在指数和与一致分布中的杰出贡献都发展和丰富了代数数论。中国数学家华罗庚等在代数数论的许多问题中也做出了重要贡献。在超越数论中，刘维尔(Liouville，J.)、贝克(Baker，A.)、罗特、盖尔丰德(Гельфонд，А.О.)、施奈德(Schneider，T.)等人的卓越工作早为国际数学界所瞩目。还值得一提的是罗特于1955年所著的《对于代数数的有理逼近》确立了有名的图埃-西格尔-罗特定理，以及贝克在超越数论方面的卓越贡献分别荣获了1958年及1970年的国际菲尔兹数学大奖.后来贝克将其研究成果整理成薄薄的128页的专著《超越数论》，被认为可与高斯的《算术研究》相媲美。

几何数论是研究一个平面或空间区域中坐标都为整数的点即整点的个数。例如，著名的圆或椭圆内的整点问题，球或椭球内的整点问题，以及除数问题等。高斯和狄利克雷(Dirichlet，P.G.L.)分别在“圆内整点问题”和“除数问题”的研究中做出了开创性的工作。以后华罗庚、维诺格拉多夫、兰道(Landau，E.G.H.)、哈代(Hardy，G.H.)等也分别得到了许多重要结果。几何数论与其他重要数论问题，如二次型理论有密切关系。

近几年，计算数论也在逐渐发展之中。

数论中的一系列重要问题，如素数分布、哥德巴赫猜想、华林问题、除数问题、圆或球内的整点问题等，都是目前正在研究的问题。特别需要指出的是，目前正在蓬勃发展的丢番图分析、 超越数论越来越引起世界上许多著名数学家的密切关注，它们已成为一个崭新的数学分支。3

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学