[科普中国]-子流形管状邻域

子流形管状邻域(tubular neighborhood ofsubmanifold)是微分拓扑中的一个工具。利用管状邻域的存在性和横截性定理，可以证明惠特尼定理：任何(无边)紧致微分流形微分同胚于欧氏空间中的解析子流形。

概念子流形管状邻域(tubular neighborhood ofsubmanifold)是微分拓扑中的一个工具。设McN是微分流形N的子流形，M'是M上的向量丛，f:E->N是嵌入映射，则(f,M')称为M在N中的管状邻域，若它适合：1. fcE是M在N中的开邻域；2.当把M等同于睿的零截面的像(cE)时，f I M一 ZM。通常也称f (M)是M在N中的管状邻域。当M,N是(无边)微分流形时，则子流形M在N中必存在管状邻域，并且M在N中的任何两个管状邻域是合痕的。利用管状邻域的存在性和横截性定理，可以证明惠特尼定理：任何(无边)紧致微分流形微分同胚于欧氏空间中的解析子流形。1

微分拓扑全称微分拓扑学。是拓扑学的一个重要的、十分活跃的分支学科。它以研究微分流形在微分同胚下的不变性质为特征。一般地，微分拓扑学是研究微分流形及微分流形之间的可微映射的性质的学科。例如，它包含有下述一些典型的问题：

1.两个微分流形在什么条件下是微分同胚的?

2.若两个微分流形是同胚的，则它们一定微分同胚吗?

3.一个微分流形能嵌入或浸入到另一个微分流形中吗?

4.怎样的微分流形是另一个带边流形的边界?

5.一个微分流形是否可平行化.

19世纪末，庞加莱(Poincaré，(J.-)H.)在代数拓扑学方面做了一系列奠基工作的同时，对3维流形的拓扑进行了深入的分析，提出了著名的庞加莱猜想：每个单连通的紧致、无边的3维流形必同胚于3维球面S。这是微分拓扑学中非常重要的、迄今尚未完全解决的问题。

20世纪以来，外尔(Weyl，(C.H.)H.)、惠特尼(Whitney，H.)、米尔诺(Milnor，J.W.)、托姆(Thom，R.)、斯梅尔(Smale，S.)、吴文俊等学者在微分拓扑学的许多方面的工作，使得这门学科得以迅速发展，并且与其他拓扑学分支，尤其是代数拓扑学建立了深刻而有力的联系。同时，微分拓扑学理论和方法上的成果推动着诸如近代微分方程、微分几何、大范围分析等数学的各个领域的发展，显示出它越来越重要的作用。2

微分流形设M是仿紧豪斯道夫 (Hau-sdorff)空间，且是拓扑流形，称A= {(Uα，Фα)|α∈P}是它的地图，如果{Uα|α∈P}是M的开覆盖，Фα是从Uα到n维欧氏空间R的某开集上的同胚。(Uα，Φα)称为坐标卡。如果两个坐标卡 (Uα，Фα)，(Uβ，Φβ) 满足Uα∩Uβ≠Φ，则称Φβ·Фα：Φα(Uα∩Uβ) →Φβ(Uα∩Uβ) 和Φα·Φβ： Φβ(Uα∩Uβ) →Фα(Uα∩Uβ) 为Uα∩Uβ上的坐标变换。如果A的所有坐标变换都是C可微的，则称A为一个C地图，其中1≤r≤∞。r也可等于ω，此时A称为解析地图。拓扑流形M的坐标卡 (U，Φ) 称为与A是Cr相容的，如果任意(Uα，Φα) ∈A，坐标变换Φ·ΦαΦα·Φ均C可微。拓扑流形M的C地图A称为最大的，如果它包含M的所有与之C相容的坐标卡。M上的最大C地图A称为M的C微分结构。(M，A)称为C微分流形，或简称为C流形。当r=∞时，C微分结构也称为光滑结构，C流形也称为光滑流形。r=ω时，C结构也称为解析结构，C流形称为解析流形。C流形(M，A)有时也简记为M。

从直观上看，拓扑流形是局部欧氏空间，局部之间用同胚映射(坐标变换)粘贴在一起。n维C流形，不仅局部同胚于n维欧氏空间，而且局部之间是用C光滑、且其逆也C光滑的坐标变换粘贴在一起。

两个C流形M和N，f：M→N是连续映射，且任一点P∈M，有包含P点的M中的坐标卡(U，Φ)以及包含f(P)的N中的坐标卡(V，)，使得f(U)⊂V，同时，映射°f°Φ-1：Φ(U)→(V)是C光滑的(1≤r≤∞或r=ω)，则称f是C映射。C映射也称为光滑映射，C映射也称为解析映射。其中称为f的局部表示。

C流形M和N之间的同胚f：M→N，如果f和f均是C映射，则称f是C微分同胚。

向量丛向量丛是流形切丛概念的抽象和推广，它是微分拓扑学和代数拓扑学的重要研究对象。设E，B是拓扑空间(B为T2空间)，π：E→B为连续满映射.ξ=(E，π，B)称为n维(实、拓扑)向量丛，若适合：

1.对于b∈B，Eb=π-1(b)是n维(实)向量空间.

2.(局部平凡性)对于b∈B，存在b的邻域U及同胚映射φ：π(U)→U×R，使得对于x∈U，φx=φ|Ex：Ex→{x}×R是向量空间的同构。

此时，B称为向量丛ξ的底空间，记为B(ξ)，E称为向量丛ξ的全空间，记为E(ξ)，Eb称为b∈B处的纤维，π称为丛射影.上述适合条件2的(U，φ)称为ξ的丛卡.ξ的一族丛卡的集合：

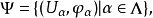若∪α∈ΛUα=B，则称为图册。进而，设B是微分流形，对于ξ的图册Φ，若α，β∈Λ，Uα∩Uβ≠，图册的转换函数gαβ：Uα∩Uβ→GL(n，R)是可微的，其中gαβ(x)=φβx°φαx：R→R，x∈Uα∩Uβ，GL(n，R)为可逆n阶方阵组成的(实)线性群，则称为可微的。若图册Φ是ξ的极大的可微图册，则ξ=(E，π，B，Φ)称为可微向量丛。此时，若B是m维微分流形，则ξ的全空间E是(n+m)维微分流形。流形的切丛、法丛、万有丛等都是可微向量丛的常见例子。向量丛ξ=(E，π，B)也称为B上的向量丛。3

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学