[科普中国]-代数集

代数集是特殊的集合，它是若干个多项式的公共根的集合，是与代数簇密切相关的概念。

定义代数集是特殊的集合，它是若干个多项式的公共根的集合，是与代数簇密切相关的概念。设 S 是域 K 上多项式环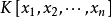 的若干个多项式的集合，记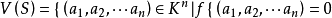，对任意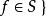为 S 中所有多项式的公共根的集合，对于 Kn 中的子集 T，若存在集合 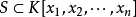使得 T=V(S)，则称 T 为一个代数集，故 V(S)=V((S))。因此，K中每个代数集皆为 V(ℜ) 的形式，其中

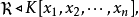称V(ℜ) 为理想 ℜ 对应的代数集。

性质代数集的交与空集合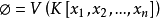 以及 Kn=V(0) 皆为代数集。反之，设 A 是Kn的一个子集合，若

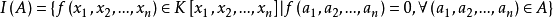
则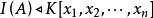 称为集合 A 对应的多项式理想。

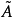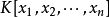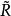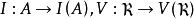另一方面，当 K 为代数闭域时，Kn 中代数集的全体与 中根理想的全体 在映射下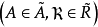 是反序一一对应的。1

代数簇代数几何学上，代数簇是多项式集合的公共零点解的集合。代数簇是经典（某种程度上也是现代）代数几何的中心研究对象。 术语簇（variety）取自拉丁语族中词源（cognate of word）的概念，有基于“同源”而“变形”之意。 历史上，代数基本定理建立了代数和几何之间的一个联系，它表明在复数域上的单变量的多项式由它的根的集合决定，而根集合是内在的几何对象。在此基础上，希尔伯特零点定理提供了多项式环的理想和仿射空间子集的基本对应。利用零点定理和相关结果，我们能够用代数术语捕捉簇的几何概念，也能够用几何来承载环论中的问题。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学