定义
如果一个基数k等于它自己的共尾度,即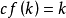 ,则称?为一个正则基数。事实上,任意满足
,则称?为一个正则基数。事实上,任意满足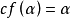 的序数(即任意非奇异序数)一定是一个基数,因此正则基数也可以定义为等于它自己共尾度的序数。
的序数(即任意非奇异序数)一定是一个基数,因此正则基数也可以定义为等于它自己共尾度的序数。
在ZFC中可以证明,任何后继基数均为正则基数(这里选择公理是必须的)。另外,0和N₀是正则极限基数。在ZFC中不能证明存在任何其他正则极限基数(weakly inaccessible cardinal),不可数的正则极限基数也称为弱不可达基数,是集合论研究中最弱的大基数。
正则性是基数的重要概念之一,它由德国数学家豪斯多夫(Hausdorff , F. ) 于1908年引入。
奇异基数[singular cardinal]
一个非正则的基数称为奇异基数,也即一个基数 k 称为奇异基数当且仅当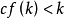 ,其中cf(k)为 k 的共尾度。
,其中cf(k)为 k 的共尾度。
在ZFC中最小的奇异基数是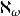 。
。
在集合论中仅次于著名的广义连续统假设的命题是如下的奇异基数假设(singular cardinals hypothesis ,SCH):对每个奇异基数 k ,若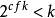 ,则
,则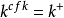 。
。
奇异基数假设比广义连续统假设弱。但和广义连续统假设一样,奇异基数假设探讨连续统函数的取值,并猜测它总是取到最小的可能值。现代集合论的研究表明,在某种大基数不存在的前提下,可以证明奇异基数假设在某些基数成立。换言之,由奇异基数假设在某些基数不成立,可以推出某些大基数存在的惊人结论。
另一方面,谢拉赫(S.Shelah)发明了pcf(可能共尾度)理论并在ZFC下证明了如下同样惊人的定理:若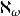 是一个强极限基数(即对所有有穷序数
是一个强极限基数(即对所有有穷序数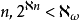 ,则
,则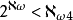 。1
。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国