[科普中国]-内模型法

内模型法(method of inner model)是集合论相对相容性证明的基本方法之一。设Σ1，Σ2为集合论语言中的两个公式集，M为Σ1的一个模型，若存在公式A(x)，使N={x|x∈M，A(x)}为Σ2的模型，则称N为M的内模型。假定Σ1相容且已知Σ1有模型M，若能在Σ1下证明存在M的一个内模型N，使N为Σ2的模型，则就证明了Σ2对于Σ1相对相容，通常把这种相对相容性证明方法称为内模型法。美籍匈牙利数学家冯·诺伊曼(J.von Neumann)于1929年最先使用内模型法证明基础公理的相容性，美籍奥地利数学家哥德尔于1938年证明连续统假设与选择公理的相容性时也是采用内模型法。1951年至1953年，谢泼德森(J.C.Shepherdson)连续发表三篇论文详细阐述了内模型方法，他指出，对可传模型而言，不能用内模型方法证明连续统假说的独立性。美国数学家科恩(P.J.Cohen)于1963年通过对内模型方法的局限性分析，发明了相容性与独立性证明的外模型方法，即力迫法。

基本介绍由哥德尔不完备性定理可知：如果ZF是协调的，则在ZF中不能证明自身的协调性。所以，在公理集合论中只考虑相对协调性问题。如：

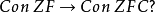
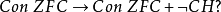解决这类问题的常用方法就是构造模型。在公理集合论中构造模型的方法不外三点：内模型法，外模型法(即力迫方法)，对称模型法。

内模型法是从已知的一个模型M出发，来定义M的一个子模型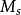，使得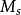满足ZF的一些公理或者ZF以外的一些公理。公理集合论的一个著名成果就是1938年K.哥德尔所给出的

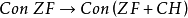的证明，证明中用的就是内模型法，但是当时尚未如此命名。迄至1951年J.C.谢泼德森已经把内模型法研究得很完善，并已知道要用此法去证明

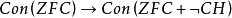是不可能的。

外模型法(即力迫法)是P.J.科恩1963年所创，科恩据此而证明了CH的相对于ZF的独立性。排列模型的想法始于弗伦克尔，当时他是用来证明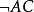及一些弱选择公理的相对协调性，适用于有原子(本元)的集合论。迭经A.莫斯托夫斯基、斯派克等人的改进而形成FMS方法，其与外模型法相结合即可构成对称模型法1。

内模型法与连续统假设连续统假设与广义连续统假设是否成立?如果成立，如何证明，这曾是集合论中的一个大问题。希尔伯特在1900年的国际数学家大会上提出的23个未解决的数学问题，作为今后数学家研究的方向，其中第一个问题便是：求证连续统假设2。

因此，连续统假设以及选择公理的研究，便是集合论中两个最大的问题，是人们注意的中心。在很长的时间内一直未能得到解决。

1938年哥德尔首先证明了，这两命题与集合论中别的公理并没有矛盾，亦即：如果上述集合论的公理系统(删去选择公理)不发生矛盾，那么添入选择公理以及广义连续统假设以后，所得的公理系统亦没有矛盾。

这是一个大突破，因为长期以来，人们对选择公理一直怀有戒心，能够不用它便不使用它；万不得已时，只好使用，但亦标明在证明中已经使用了选择公理，人们这样做，是因为万一有一天证明了选择公理不合用，可以随时抛弃它，而没有使用它的部分便可以很安然地保存下来了。经过哥德尔的证明，人们放心了，至少对选择公理不抱敌意的人可以放心了，只要别的部分没有问题，那么选择公理亦是没有问题的。

哥德尔的证明方法大体如下：如果别的公理没有矛盾，那么可以作出一个模型，在其中别的公理是成立的。在这个模型中，可以发展序数论。于是，可以按照一定的办法作出足够多的序数(良序集)。然后，我们把这些序数的全体作成一个新模型，在这个新模型中，不但集合论的别的公理继续成立，而且选择公理(甚至于很强的选择公理，所谓全局选择公理)成立，广义连续统假设亦成立。既然有一模型(新模型)满足这些公理，那么它们当然是不矛盾的了。

哥德尔的方法叫做内模型法，其方法是(假设某些公理不矛盾)先造出一个模型，满足某些公理，再对这个模型加些限制，从而得出一个更小的模型(内模型)，它不但满足原来的公理而且还满足一些新公理，因而证明了，把这些新公理添到原来的公理去时，只要原来的公理没有矛盾，那么添入后亦不会发生矛盾。

但是，连续统假设乃至于选择公理，能够不能够由别的集合论公理推出来呢?这正是康托儿原来的想法，他宣称他已经推出了连续统假设，不日即将发表，后来一直没有发表，大概他知道他原来所作的证明不完整之故。

1963年，科恩(P.J.Cohen)证明了，由集合论中别的公理推不出选择公理，别的公理加入选择公理后推不出连续统假设，加入连续统假设后仍推不出广义连续统假设。换言之，它们都是推不出来的，亦即把它们的否定加入以后，是不会发生矛盾的。

科恩详细地论述了，要证明选择公理和连续统假设的独立性，是不能使用内模型法的，必须使用一种新的方法，叫做力迫法。力迫法的理论比较艰深，我们这里就不多介绍了，只是指出，力迫法是一个很重要的方法，利用它，不但证明了选择公理和(广义)连续统假设是独立于别的集合论公理的，而且数学上好些独立性问题，以前长久以来一直未能解决的，借助于力迫法后，也一一得到了解决(总共有五、六十个问题之多)。可以说，力迫论的出现，是数理逻辑(尤其是集合论)的一个重要的进步。后来，力迫论又有新发展，出现了各种力迫论，固有力迫论，迭代力迫论等等，都受到人们的注意。

根据哥德尔与科恩的两个结果，可以知道，在集合论别的公理之上，加入选择公理或其否定，可以分别得到一个不矛盾的公理系统，加入连续统假设或其否定，亦可以分别得到一个不矛盾的公理系统。因此，集合论类似于几何学，在绝对几何的公理之上，加入欧几里得平行公理或其否定，可以分别得到一个不矛盾的公理系统，那便是欧几里得几何及非欧几里得几何2。

公理集合论公理集合论(axiomatic settheory)是数理逻辑的主要分支之一，是用公理化方法处理朴素集合论的内容的理论，更重要的，是研究集合论的元数学性质——集合论的模型、各公理的关系、各系统之间的关系、各种不可判定语句，以及集合论公理化过程中所提出的种种新方法和新问题的理论3。

1908年策梅罗提出了第一个集合论公理系统，旨在避免集合论中的悖论，20年代弗伦克尔和斯科朗加以改进和补充，得到常用的策梅罗-弗伦克尔公理系统，简记为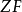。这是一个建立在有等词和属于关系的一阶谓词演算之上的形式系统。它的非逻辑公理有：外延公理、空集公理、无序对公理、并集公理、幂集公理、替换公理模式、正则公理。如果另加选择公理(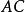)则所得到的公理系统简记。

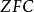已经证明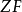，对于发展集合论是足够的，它能避免已知的集合论悖论。并在数学基础研究中提供一种方便的语言和工具。在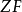中，几乎所有的数学概念都能用集合论语言表达。数学定理也大都可以在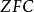系统内得到形式证明。因而作为整个数学的基础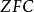，是完备的。数学的无矛盾性可归结为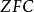的无矛盾性。 ·

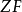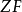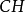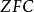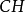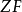由哥德尔不完全性定理可知，如果是无矛盾的，则在中不能证明自身的无矛盾性。所以，在公理集合论中只考虑相对无矛盾性问题，解决的方法是构造模型。常用三种方法：内模型法，外模型法(力迫****方法)，对称模型法。1938年，哥德尔证明了对于的相对无矛盾性，用的就是内模型法。1963年，科恩创立外模型法，证明了相对于的独立性。

公理集合论的一个研究领域是由朴素集合论中对无穷组合问题的研究发展而来的组合集合论。另一个研究领域是描述集合论(谱系理论)，主要探讨划分层次(级)后的实数子集的结构性质问题。在研究这两个领域的许多问题时，都要用到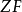(或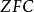)以外的附加假设(公理)才能判定。常用的附加假设有：可构成公理，各种大基数公理，以及与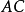不相容的决定性公理等。

1938年，哥德尔提出了可构成公理，60-70年代，这一公理得到重视和发展。大基数公理虽然早已提出[在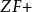大基数公理(即“存在一大基数”)的公理系统中，可以证明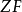是无矛盾的]，但直到60年代以后才作为公理集合论某一领域的附加假设使用。几乎每一种大基数都是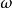的某种性质向不可数基数的推广。可构成性、大基数和力迫方法(外模型法)已成为当代公理集合论研究的三大主流，它们又是三种重要的工具。随着无穷对策的产生和对策论在数学各分支的渗透，决定性公理也日益受到重视3。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学