[科普中国]-柯尔莫哥洛夫强大数律

柯尔莫哥洛夫强大数律(Kolmogorov strong law of large numbers)是最重要最常用的强大数律。若{Xn}为独立同分布随机变量序列，EXn存在，则以概率1成立n个独立同分布随机变量X1，X2，...，Xn的平均值随n增大几乎趋于μ。

基本介绍柯尔莫哥洛夫强大数律是指若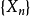为独立同分布随机变量序列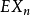，存在，则以概率1成立。

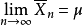大数律中涉及到的随机变量序列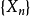也可以不是相互独立的。特别对于平稳序列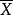，可看为序列按时间的平均，而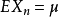是同一时刻不同样本的统计平均。这时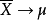，表明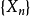随时间的增长遍历了它的各种可能状态，因而使“时间平均”向“统计平均”收敛。这又称为平稳序列的遍历性，它也是一种大数律。在平稳过程理论中，辛钦和G.D.伯克霍夫分别建立了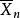向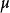均方收敛和以概率1收敛的遍历定理。

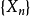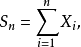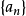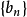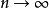不仅有算术平均向常数收敛的大数律，更一般地，对随机变量序列，若存在常数序列及趋于无穷的，当时使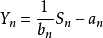依概率或以概率1收敛于零，则分别称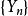是依概率稳定或以概率1稳定的。这是大数律的一种推广形式。由于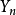依概率收敛于零与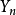的分布向集中于零的退化分布弱收敛是等价的，因此弱大数律就是讨论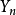的分布向退化分布弱收敛的极限定理（见中心极限定理），可作为普遍极限定理的特例来处理1。

两种情形1. 设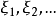相互独立，而且有有穷方差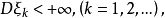如果

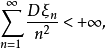则随机变量列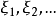服从强大数律，即

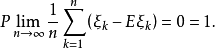
2. 设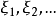相互独立同分布，如果数学期望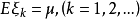有穷，则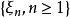服从强大数律，即

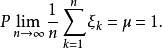
这两个定理是由俄国数学家柯尔莫哥洛夫(Колмогоров，А.Н.)最早得到的2。

大数律概率论中陈述随机变量序列的算术平均值向常数收敛的定律。是概率论与数理统计学的基本定律之一。

当投掷一枚正常的钱币时，如果重复次数非常大，就会发现其中出现正面与反面的次数近于相等。由于误差不可避免，钳工师傅要精确测量一个工件的尺寸时，先测足够多次，再取各次测量的算术平均值，就能得到满足精度要求的工件尺寸。

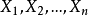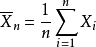一般地讲，n个独立同分布随机变量的平均值随n增大几乎趋于它们的共同数学期望，这叫独立同分布随机变量序列的大数定律。在更一般的情形里，涉及的随机变量也可以不是独立同分布的。大数律有多种形式，如辛钦大数律、柯尔莫哥洛夫****强大数律及各种随机序列或随机过程的大数律等等3。

柯尔莫哥洛夫柯尔莫哥洛夫(1903-1987)是苏联数学家。1920年起就学于莫斯科大学，1922年在校期间完成关于傅里叶级数、解析集合的著名论文。其后连续发表了许多重要的研究成果。1925年毕业后，留校任研究助理，开始研究独立随机变量的级数收敛问题及发散时的阶数，提出了著名的柯尔莫哥洛夫0-1律、柯尔莫哥洛夫不等式、辛钦-柯尔莫哥洛夫三级数定理、柯尔莫哥洛夫强大数律、柯尔莫哥洛夫判别法、柯尔莫哥洛夫谱等。1929年发表论文《测度的一般理论和概率论》，提出概率的公理化定义。用测度论的语言将概率论确立为现代数学的一个领域是其在概率论方面的一大功绩。1931年任莫斯科大学教授。1939年成为苏联科学院院士。在《概率论的解析方法》中详尽阐述了无后效随机过程理论的原理，建立了马尔可夫过程的理论，标志着概率论发展的一个新时期。从20世纪50年代中期起的研究转向信息动力系统理论、信息论、函数论的内在联系、希尔伯特第13问题、有限自动机等方面，都得到了奠基性的结论4。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学