[科普中国]-强拟凸函数

简介

若对任意的x,y∈ C，x≠ y，及任意λ∈ (0,1)，有

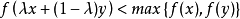
则称f(x)为C上的强拟凸函数。

我们知道，在数学规划的理论及算法中，函数的凸性只是一个充分条件，而不是必要条件。如何推广函数的凸性概念，使得凸规则的大多数结果能推广到非凸规划，已构成了数学规划研究领域的当前趋势之一。拟凸函数是一类非常重要的广义凸函数，已有大量文献对此作了研究。讨论拟凸函数、严格拟凸函数及强拟凸函数之间的关系，得到新结果，使得某些结论成为直接推广。

基本概念拟凸函数

直观的看，函数f（x）是拟凸的表示曲线ACB之间的点都低于B点。显然，如果函数f（x）是凸的，则图形如一个正放的锅，弦在曲线上面，而弦上的点本身满足上述性质，因而一定是拟凸的。代数的证明只要利用两者的定义即得。但反向则不一定成立，如同是单调的函数的凹函数、线性函数、凸函数的图形中，同样满足拟凸函数的定义，即拟凸函数可以是凹函数，也可以是凸函数。

与拟凹函数相对，拟凸函数也有一个等价定义：如果函数f（x）是拟凸的，当且仅当集合S1={x|f（x）≤c}是凸集，我们称集合S1为函数f（x）的下等值集（Lower Contour Set）。

若对任意的x,y∈ C,x≠ y，及任意λ∈ (0,1)，有

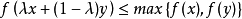
则称f(x)为C上的拟凸函数。1

严格拟凸函数

若对任意的x,y∈ C,x≠ y，f(x)≠f(y)，及任意λ∈ (0,1)，有

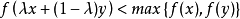
则称f(x)为C上的严格拟凸函数。

引理

设f(x)为C上的下半连续函数，则f(x)为C上的强拟凸函数的充要条件是：

对任意的x,y∈ C，x= y，存在λ∈ (0,1)(λ依赖于x,y)，使得

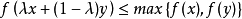
定理

设f(x)为C上的下半连续函数，则f(x)为C上的强拟凸函数的充要条件是：

对任意的x,y∈ C，x≠ y，存在λ∈ (0,1)(λ依赖于x,y)，使得

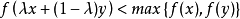
证明：必要性显然成立。下面证明充分性，用反证法。

若存在x1,x2∈ C，x1≠ x2，及T0∈(0,1)，使得

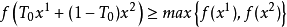
由假设条件及引理知f(x)为C上的拟凸函数，故有

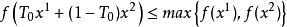
故

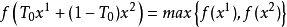
不失一般性，不妨设f(x2)≥ f(x1)

若f(x2)> f(x1)，令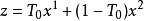，则

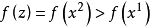
由假设知，存在λ0∈ (0,1)，使得

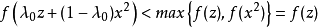
则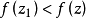

显然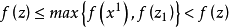，矛盾!证毕。2

严格拟凸函数成为强拟凸函数的条件

若f(x)为C上的严格拟凸函数，若对任意的x,y∈ C,x≠ y，x≠y，f(x)=f(y)，存在λ∈ (0,1)，有

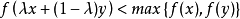
则f(x)为C上的强拟凸函数。