概念
克罗内克指数(Kronecker index)是一种特定的指标。设M是闭连通光滑n维流形。利用模2系数,存在一个基本同调类μM∈Hn(M,Z/2),故对任意上同调类V∈H(M,Z/2),定义克罗内克指数为:1
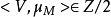
流形流形是一类特殊的连通、豪斯多夫仿紧的拓扑空间,在此空间每一点的邻近预先建立了坐标系,使得任何两个(局部)坐标系间的坐标变换都是连续的。n维流形的概念在18世纪法国数学家拉格朗日的力学研究中已有萌芽。19世纪中叶英国数学家凯莱(1843)、德国数学家格拉斯曼(1844,1861)、瑞士数学家施勒夫利(1852)分别论述了n维欧几里得空间理论,把它视为n个实变量的连续统。1854年德国数学家黎曼在研究微分几何时用归纳构造法给出一般n维流形的概念:n维流形是把无限多个(n-1)维流形按照一维流形方式放在一起而形成的,从此开始流形的拓扑结构及其局部理论的研究。法国数学家庞加莱在19世纪末把n维流形定义为一种连通的拓扑空间,其中每一点都具有和n维欧氏空间同胚的邻域(被称为庞加莱流形),从而开辟了组合拓扑学的道路。
对流形的深入研究集中在流形上的微分结构与组合结构的存在性、唯一性问题,微分结构与组合结构的关系,流形的各种意义下的分类等问题,20世纪50—60年代做出许多重要结果,近几十年来出现有限维带边流形和无限维流形概念。流形理论在与其他拓扑理论的相互结合发展中也提出许多问题,其研究仍在继续。
流形也是一类拓扑空间,它在每一点的附近都与欧氏空间同胚。一般的流形概念,起始于对于可微流形的研究,在点集拓扑中已经熟悉把一元或多元连续函数的概念,推广为拓扑空间之间连续映射的概念。但是对于函数的可微性,在进行类似的推广时,却遇到截然不同的情况,若M,N为拓扑空间,f:M→N为映射,则为了计算微商,须考虑(f(x+h)-f(x))/h,然而在一般空间中,这是没有意义的,因此对于M与N,提出了有一个支撑空间的要求,这是产生可微流形概念的客观要求。
在历史上,n维流形的概念在拉格朗日(Lagrange,J.-L.)时代已初见端倪,黎曼(Riemann,G.F.B.)于1854年利用参数的观点,对维数用归纳法进行构造,以后庞加莱(Poincaré,(J.-)H.)为了摆脱这种研究方法的复杂性,把n维流形定义为现在这个样子,即它是一种连通的拓扑空间,其中每点有一个邻域与R(或C)的一个邻域同胚,即把流形定义为局部欧氏空间。这是曲线与曲面概念的高维推广,它是代数拓扑、微分拓扑、几何拓扑以及微分几何研究的主要对象。
上同调类上同调类的概念可以由上同调模的概念得出。上同调模是一种重要的模。指由上复形给出的模。设:
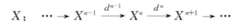
是环A上的复形,因为dd=0,所以Im dker d,于是H(X)=ker d/Im d为A模,称此模为上复形X的上同调模。分别以Z(X),B(X)来表示ker d,Im d,把X,Z,B,H的元素分别称为上链、上循环、上边缘、上同调类。若X是环A上的复形,则对偶地可以定义复形X的同调模Hn(X)=ker dn/Im dn+1,把Xn,Zn,Bn,Hn的元素分别称为链、循环、边缘、同调类。2
人物简介———克罗内克克罗内克是一位德国数学家。生于利格尼茨,卒于柏林。1841年入柏林大学,选学数学、天文、化学和哲学等课程,曾参加学生的民主活动。1845年以关于代数数域的研究论文获博士学位。之后返乡继承遗产,经营田庄和银行,其间仍以研究数学自娱。1855年重返柏林,以很快的速度发表一系列论文,内容涉及数论、椭圆函数论和代数学,特别探讨了这些学科的相互依赖性。1861年被选为柏林科学院院士。1883年受聘为柏林大学教授。1884年当选为英国皇家学会会员。他还是法国科学院和圣彼得堡科学院外籍院士。克罗内克的主要贡献在数论、代数学、函数论、拓扑学等方面;努力统一数论、代数学和分析学的研究;深入探讨椭圆模函数理论,并用它解出了一般的五次方程;发展了库默尔的“理想数”理论,创立了有理函数域论,引进了在域上添加代数量生成扩域的概念和模系的概念,因而使代数数的理论独立于代数基本定理;发现有理数域的任一阿贝尔扩张一定是一分圆域的子域,并提出著名猜想(见克罗内克青春之梦):椭圆函数具有复数乘法的模方程与虚二次域的阿贝尔扩张有类似性。他还提出研究代数曲线的重要方法。在数学基础的大论战中,他是直觉主义数学流派的代表人物之一,曾激烈反对过外尔斯特拉斯和G.康托尔等人的观点,主张数学的算术化。他的数学观对后世有极大影响。他的一句名言是:“上帝创造了整数,其他一切都是人为的。”反映了他对当时的分析学持批判态度。他的著作由亨泽尔编辑,以《克罗内克全集》(5卷,1895—1931)出版。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国