经典的Tobit 模型是James Tobin在分析家庭耐用品的支出情况时对Probit 回归进行的一种推广(Tobit一词源自Tobin’S Probit),其后又被扩展成多种情况,Amemiya将其归纳为Ⅰ型到Ⅴ型Tobit模型。标准的Ⅰ型Tobit回归模型如下:
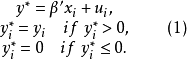 式(1)中,
式(1)中,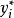 是潜在应变量,潜变量大于0时被观察到,取值为
是潜在应变量,潜变量大于0时被观察到,取值为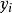 ,小于等于0时在0处截尾,
,小于等于0时在0处截尾,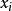 是自变量向量,
是自变量向量,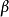 是系数向量,误差项
是系数向量,误差项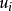 独立且服从正态分布:
独立且服从正态分布: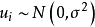 。该模型也可以作如下简化表达:
。该模型也可以作如下简化表达:
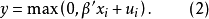
用最小二乘法估计含有截尾数据的模型参数会产生偏差,且估计量是不一致的。在一定假设下可通过最大似然法估计其参数1。
Tobit模型的最大似然估计当Tohit模型的误差项满足正态性和方差齐性时,即式(1)中,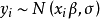 ,潜变量
,潜变量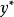 满足经典线性模型假定,服从具有线性条件均值的等方差正态分布。在该假设条件下,Tobit模型中对于正值即
满足经典线性模型假定,服从具有线性条件均值的等方差正态分布。在该假设条件下,Tobit模型中对于正值即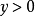 ,给定x下y的密度与给定x下
,给定x下y的密度与给定x下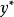 的密度一样;对于
的密度一样;对于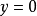 的观测值,由于u/a服从标准正态分布并独立于丁,则
的观测值,由于u/a服从标准正态分布并独立于丁,则
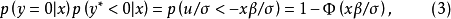 因此如果
因此如果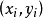 是来自总体的一次随机抽取,则在给定
是来自总体的一次随机抽取,则在给定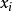 下
下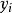 的密度为:
的密度为:
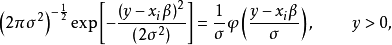
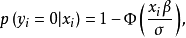 式中,
式中,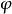 是标准正态密度函数。从中得到每个观测i的对数似然函数:
是标准正态密度函数。从中得到每个观测i的对数似然函数:
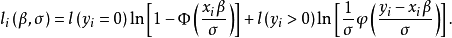 通过将上式对i求和,就可以得到容量为n的一个随机样本的对数似然函数,即
通过将上式对i求和,就可以得到容量为n的一个随机样本的对数似然函数,即
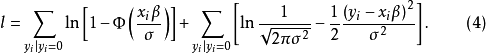 该式由两部分组成,一部分对应于没有限制的观测值,是经典回归模型部分;一部分对应于受到限制的观测值。这是一个非标准的似然函数,它实际上是离散分布与连续分布的混合。通过对上式极大化,就可以得到
该式由两部分组成,一部分对应于没有限制的观测值,是经典回归模型部分;一部分对应于受到限制的观测值。这是一个非标准的似然函数,它实际上是离散分布与连续分布的混合。通过对上式极大化,就可以得到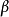 和
和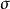 的最大似然估计值。该对数似然函数的求解比较棘手,因为Tobit 模型的对数似然函数对原参数
的最大似然估计值。该对数似然函数的求解比较棘手,因为Tobit 模型的对数似然函数对原参数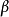 和
和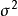 不是全局凹的(global concavity)。对该似然函数进行再参数化,可使得估计过程更为简单,并且再参数化后的对数似然函数是全局凹的。令
不是全局凹的(global concavity)。对该似然函数进行再参数化,可使得估计过程更为简单,并且再参数化后的对数似然函数是全局凹的。令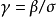 和
和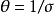 对数似然函数变为
对数似然函数变为
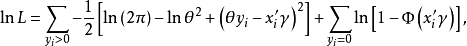 对上式极大化,由于Hessian矩阵始终是负正定的,所以不管初始值是什么,只要迭代过程有一个解,则这个解就是似然函数的全局最大化解。应用牛顿法求解时较为简单,且收敛速度快,得到
对上式极大化,由于Hessian矩阵始终是负正定的,所以不管初始值是什么,只要迭代过程有一个解,则这个解就是似然函数的全局最大化解。应用牛顿法求解时较为简单,且收敛速度快,得到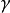 和
和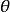 的估计量后,再利用
的估计量后,再利用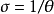 和
和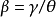 求得原参数估计量。这些估计量的渐近协方差矩阵可以从估计量
求得原参数估计量。这些估计量的渐近协方差矩阵可以从估计量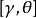 中得到1。
中得到1。
Tobit模型最大似然估计的一致性依赖于其潜变量模型中误差项的正态性和方差齐性,在误差项存在序列相关(serial correlation)的情况下最大似然估计仍可以保持一致性,但其异方差和非正态分布会导致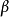 和
和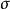 的不一致估计。检验Tobit模型中误差项是否服从正态分布的方法有Hausman检验、拉格朗日乘数检验和条件矩检验等。不满足正态分布时可选用替代的其他分布,如指数分布、对数正态分布和威布尔分布。但是假定一些其他的特定分布并不能有效的解决问题而且有可能使问题更糟,此时可采用一些稳健的半参数方法。
的不一致估计。检验Tobit模型中误差项是否服从正态分布的方法有Hausman检验、拉格朗日乘数检验和条件矩检验等。不满足正态分布时可选用替代的其他分布,如指数分布、对数正态分布和威布尔分布。但是假定一些其他的特定分布并不能有效的解决问题而且有可能使问题更糟,此时可采用一些稳健的半参数方法。
删失最小绝对离差估计CLAD(censored least absolute deviations)是Tobit模型的一种半参数估计方法,该方法假定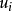 的中位数为0,即
的中位数为0,即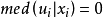 ,这也意味着
,这也意味着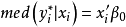 ,如果额外假设误差项有关于0为中心的对称分布,那么条件中位数和均数就是一致的。对于经典线性模型,最小绝对离差估计LAD(Least Absolute Deviations)通过最小化误差项的绝对值之和来获得回归系数的估计值(最小一乘估计)。在Tobit 模型中只能观测到截取的因变量y所以要对经典的LAD估计作一些改进。对任何连续随机变量Z,可以通过选择合适的b作为Z 分布的中位数从而最小化函数,
,如果额外假设误差项有关于0为中心的对称分布,那么条件中位数和均数就是一致的。对于经典线性模型,最小绝对离差估计LAD(Least Absolute Deviations)通过最小化误差项的绝对值之和来获得回归系数的估计值(最小一乘估计)。在Tobit 模型中只能观测到截取的因变量y所以要对经典的LAD估计作一些改进。对任何连续随机变量Z,可以通过选择合适的b作为Z 分布的中位数从而最小化函数,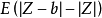 。如果
。如果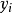 的中位数是回归自变量和未知参数的已知函数
的中位数是回归自变量和未知参数的已知函数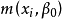 ,那么
,那么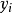 的样本条件中位数可以通过选择适当的
的样本条件中位数可以通过选择适当的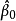 来获得,而这个
来获得,而这个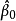 使得函数
使得函数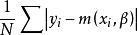 在
在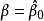 处最小化。对于截取回归模型来说,很容易证明
处最小化。对于截取回归模型来说,很容易证明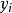 的中位数函数
的中位数函数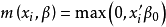 ,所以CLAD估计的目标函数为
,所以CLAD估计的目标函数为
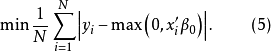 由于该函数是连续的,最小值总是存在,但最小化可能产生不唯一的
由于该函数是连续的,最小值总是存在,但最小化可能产生不唯一的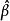 值。CLAD估计具有一致性,并且有渐近的正态分布,由于最小化的函数不是连续可微的,所以该估计量的计算较复杂。Buchinsky 建议用迭代线性规划算法ILPA(the iterative linear programming algorithm)来获得CLAD 的估计量。由于CLAD 估计允许误差项可以为更广泛的分布,包括非对称分布,当Tobit模型的某些有关分布的假设不成立时,,蒙特卡罗模拟证据表明它表现良好,对异方差也稳健。Deaton指出当有异方差性时,小样本情况下,CLAD估计有大的标准差,而似然估计在小样本中尽管有偏倚,但它的标准差较小。所以对于小样本来说似然估计是比较好的,而CLAD估计随着样本含量的增大比较适用1。
值。CLAD估计具有一致性,并且有渐近的正态分布,由于最小化的函数不是连续可微的,所以该估计量的计算较复杂。Buchinsky 建议用迭代线性规划算法ILPA(the iterative linear programming algorithm)来获得CLAD 的估计量。由于CLAD 估计允许误差项可以为更广泛的分布,包括非对称分布,当Tobit模型的某些有关分布的假设不成立时,,蒙特卡罗模拟证据表明它表现良好,对异方差也稳健。Deaton指出当有异方差性时,小样本情况下,CLAD估计有大的标准差,而似然估计在小样本中尽管有偏倚,但它的标准差较小。所以对于小样本来说似然估计是比较好的,而CLAD估计随着样本含量的增大比较适用1。
在实际应用中,Tobit 回归系数的解释和一般线性模型的归系数不同。它与Tobit模型中三个重要的条件期望(conditional expectation)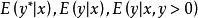 有关,具体应该是哪个解释取决于实际应用的目的,将这些条件期望对协变量进行求导后就是想要得到的边际效应(marginal effects)。
有关,具体应该是哪个解释取决于实际应用的目的,将这些条件期望对协变量进行求导后就是想要得到的边际效应(marginal effects)。
在Tobit 模型中可以用似然比检验检验回归系数,既适合单个自变量的假设检验又适合多个自变量的同时检验。
似然比检验基于不受约束模型和受约束模型的对数似然函数之差。其思想是,由于似然估计最大化了对数似然函数,所以去掉变量一般会导致一个较小的对数似然函数值。对数似然函数值的下降程度是否大到足以断定去掉的变量是重要的,可以通过似然比统计量和一系列临界值做出判断。似然比统计量是对数似然值之差的2倍即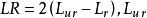 为不受约束模型即含有待检因素的Tobit 模型的对数似然值,
为不受约束模型即含有待检因素的Tobit 模型的对数似然值,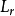 为受约束模型即不包含待检因素的Tobit 模型的对数似然值。似然比统计量在
为受约束模型即不包含待检因素的Tobit 模型的对数似然值。似然比统计量在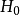 下服从渐近
下服从渐近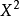 分布,自由度为待检参数的个数q。
分布,自由度为待检参数的个数q。
以上介绍中将截尾点设为0,这并不使得该模型失去一般性,事实上截尾临界点可以为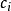 ,
,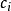 可以对所有的i 都是一样的,但在多数情况下随着i的特征而变化,并且
可以对所有的i 都是一样的,但在多数情况下随着i的特征而变化,并且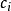 既可以从左边截尾也可以从右边截尾还可以两边同时截尾。事实上,当误差项指定为生存时间经常服从的指数分布且为右删失时,起源于计量经济学中的Tobit模型就是医学统计学领域常用的生存分析中的一种加速失效模型(accelerated failure model)1。
既可以从左边截尾也可以从右边截尾还可以两边同时截尾。事实上,当误差项指定为生存时间经常服从的指数分布且为右删失时,起源于计量经济学中的Tobit模型就是医学统计学领域常用的生存分析中的一种加速失效模型(accelerated failure model)1。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国