[科普中国]-数表示法

用一位二进制位表示数的符号：0表示正数，1表示负数，这种表示数的方法，称为带符号数的表示方法。所表示的数，叫做带符号的数。带符号的数其最高位为符号位。

如果将全部有效位都用来表示数的大小，这种数的表示方法，叫无符号数的表示方法，所表示的数，叫无符号数。

真值就是利用"+"、"-"表示数的符号，数值部分为数的绝对值。例如：N1=+1101001B= +105；N2=-1101001B=-105。数的真值可以使用二进制形式、八进制形式、十进制形式或十六进制形式表示。

机器数就是在机器中用最高位表示数的符号，其它位表示数值的大小。这时最高位叫做符号位，规定用“0"表示正，“1’’表示负。这样对于n位二进制数，如果它是一个带符号的数，则最高位Bn-1就表示数的符号，剩下的n-1位表示数的大小。简单的说，机器数就是数据在机器中的二进制表示形式，机器数所表示的值称为该机器数的“真值”。

例如：一个带符号的数11101001B，最高位"1"为符号位，代表“-”其它位为数的值，它的真值为：-1101001B(-105)。

对于任意一个数(十进制数)都可以表示成按权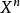(n为整数)展开的多项式，这里X称为基数。对于不同的X，形成相应的X进制数。X进制数只包含数字符号0,1，...，X-1，并且在运算过程中“逢X进一，借一当X”。常用的X进制数有二进制数、八进制数、十进制数和十六进制数。其中，十六进制包含数字符号0，1，...，9，A，B，C，D，E，F。

例如，对于数210分别用二进制、八进制、十进制、十六进制表示如下：

二进制：210=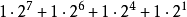=11010010(B)；

八进制：210==322(O)

十进制：210=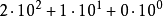=210(D)

十六进制：210==D2(H)

机器数在计算机中的表示方法有三种，即原码、反码和补码，最常用的是原码和补码两种，原码表示法比较直观，补码运算则比较简单。

原码表示法是一种直观的机器数表示法，用最高位表示符号，符号位为0表示该数为正，符号位为1表示该数为负，有效数值部分用二进制绝对值表示。如真值为+0.1010和-1100其原码为0.1010和11100。用原码作乘除法时，可取其绝对值(尾数)直接运算，再按同号相乘除为正，异号相乘除结果为负的原则单独处理符号，但对常用的加减法运算，却极不方便，由此引进补码的概念。

补码是让数的符号位也作为数的一部分参与运算，使实际操作仅与指令规定的操作性质有关，而与数的符号无关。即确定一个数作模以后，将某数X对模M的补数称为X的补码，表示为[X]补=M+X (Mod M)，正数的补码与原码一样，但是舍去了模。如x=0.101，[x]补=0.101 (mod 2)，对于负数，补码的尾数与原码不同，其符号位在形式上与原码相同，也用1表示负数，但这个1是通过模获得的，也是数值的一部分，可与尾数一起参与运算，如x=-0.101，则[x]补=2+(-0.101)=1.011 (mod 2)。

对补码的求值，一般是通过原码转化而来。对正数，[x]原=[x]补；对负数，符号位保持不变，尾数各位变反，然后末位加1，即“变反加1”。如：[x]原=1.1010，则[x]补=1.0110。

反码表示法仅对尾数逐位取反而不在末位加1，它可以达到化减为加的目的。正数反码与原码、补码相同，负数反码的符号位为1，其尾数可由其绝对质逐位反而得，符号位也参与计算。具体表示为：x=0.101，x反=0.101；x=-0.101，x反=1.010。

计算机中，小数点的表示有两种方法，即定点和浮点表示法。

对于数，其中，N代表数字，S代表尾数，R代表基数，e代表阶码，即小数点的实际位置。

定点表示法中，e的取值固定不变。定点表示法中有下述两种方法：

(1) 纯小数表示法：数符·尾数；

(2) 整数表示法：数符 尾数。

定点表示法具有如下缺点：

(1) 表示的数据范围小；

(2) 使用不方便，运算精度低，浪费存储单元。

定点数的分辨率为：在字长为n+1的计算机中。纯小数的分辨率为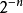，纯整数的分辨率为1。

浮点表示法中，小数点的位置是不定的，可以浮动。一个二进制数可表示为：N=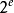·S，其中S为数N的尾数，表示数N的有效值，用Sf表示尾数的符号，Sf=0为正数，Sf=1为负数；e为数N的阶码，表示小数点的位置，用表示阶码的符号，=0为正数，=1为负数。

具体用二进制数表示为：。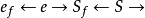

浮点数数据范围：

(1) 最大正数和最小正数的区间，称为正数区；

(2)最小负数和最大负数的区间，称为负数区；

(3)最大负数和最小正数之间的区域，由于绝对值小于可表示的值。所以称为下溢区，一般用0表示。称为机器零。

(4)处于最大正数和最小负数之外的区间，称为上溢区。最大正数以外称为正溢区，最小负数以外称为负溢区。1