数据分析是一类统计方法,其主要特点是多维性和描述性。有些几何方法有助于揭示不同的数据之间存在的关系,并绘制出统计信息图,以更简洁的解释这些数据中包含的主要信息。其他一些用于收集数据,以便弄清哪些是同质的,从而更好地了解数据。数据分析可以处理大量数据,并确定这些数据最有用的部分。
在数据分析中,抽样是指:从全部数据中选择部分数据进行分析,以发掘更大规模数据集中的有用信息。例如,假设有一片占地 100 英亩且其中树木分布非常均匀的区域,如果您要估算该区域的树木数量,则可以统计一英亩的树木数量,然后用所得数值乘以 100,或者统计半英亩的树木数量,然后用所得数值乘以 200,从而得出可准确代表整个 100 英亩区域树木数量的结果。抽样数据方式简单来说是指通过抽样技术选出数据符合分析模型要求或算法要求的方式。
抽样概述在统计学中,抽样(Sampling)是一种推论统计方法,它是指从目标总体(Population,或称为母体)中抽取一部分个体作为样本(Sample),通过观察样本的某一或某些属性,依据所获得的数据对总体的数量特征得出具有一定可靠性的估计判断,从而达到对总体的认识。
概率抽样方法简单随机抽样(simple random sampling),也叫纯随机抽样。从总体N个单位中随机地抽取n个单位作为样本,使得每一个容量为样本都有相同的概率被抽中。特点是:每个样本单位被抽中的概率相等,样本的每个单位完全独立,彼此间无一定的关联性和排斥性。简单随机抽样是其它各种抽样形式的基础。通常只是在总体单位之间差异程度较小和数目较少时,才采用这种方法。
系统抽样(systematic sampling),也称等距抽样。将总体中的所有单位按一定顺序排列,在规定的范围内随机地抽取一个单位作为初始单位,然后按事先规定好的规则确定其他样本单位。先从数字1到k之间随机抽取一个数字r作为初始单位,以后依次取r+k、r+2k……等单位。这种方法操作简便,可提高估计的精度。
分层抽样(stratified sampling)。将抽样单位按某种特征或某种规则划分为不同的层,然后从不同的层中独立、随机地抽取样本。从而保证样本的结构与总体的结构比较相近,从而提高估计的精度。
整群抽样(cluster sampling)。将总体中若干个单位合并为组,抽样时直接抽取群,然后对中选群中的所有单位全部实施调查。抽样时只需群的抽样框,可简化工作量,缺点是估计的精度较差。1
非概率抽样方法方便抽样(Convenience Sampling)。调查者以自己方便的方式抽取偶然得到的样本,最典型的方便抽样是“街头拦人法”。方便抽样的优点是易于实施,代价较小,缺点是样本代表性差,有很大的偶然性。
定额抽样(Quota Sampling)。调查者先将总体按某种特征划分成不同的组,然后在配额内以主观判断选定样本作为研究对象。定额抽样和分层抽样的相同之处是对总体进行分组,不同之处是分层抽样按概率原则在层内抽选样本,而定额抽样选取样本是主观的。定额抽样的优点是能够缩小抽样范围,减少抽样成本,缺点是确定额度困难,需多次探索。
判断抽样(Judgement Sampling)。研究人员根据调查目的和主观经验,从总体中选择最具代表性的样本。判断抽样的优点是可以用于总体难以确定的研究对象,缺点是受研究人员的主观倾向性影响大,一旦主观判断失误, 则易引起较大的抽样偏差。
滚雪球抽样(Snowball Sampling)。先选取若干符合特征的样本构成最初的调查对象,然后依靠他们提供新的调查对象,随着调查的推进,样本如同滚雪球般由小变大,滚雪球抽样方法的优点是能够很方便地找到被调查者,用于探索性研究,缺点是样本之间必须存在联系且愿意保持和提供这种联系。2
评估方法的抽样数据方式通常,可通过实验测试来对学习器的泛化误差进行评估并进而做出选择,测试样本是从样本真实分布中独立同分布抽样而得,测试集应该尽可能与训练集互斥,即测试样本尽量不在训练集中出现,未在训练过程中使用。
留出法(hold-out)方法:直接将数据集D划分为两个互斥的集合,训练集合S和测试集合T,在S上训练模型,用T来评估其测试误差。注意:训练/测试集的划分要尽可能保持数据分布的一致性,避免因为数据划分过程引入额外的偏差而对最终结果产生影响。
缺点与改进:单次使用留出法得到的估计往往不够稳定可靠,在使用留出法时,一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果
实际运用:实际中一般将大约2/3~4/5的样本用于训练,剩余样本用于测试。3
交叉验证法(cross validation)方法:先将数据集D划分为k个大小相似的互斥子集.每个子集Di都尽可能保持数据分布的一致性,即从D中通过分层采样得到 .然后每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,这样就可以获得k组训练/测试集,从而可以进行k次训练和测试,最终返回的是这k个测试结果的均值。
实际运用:一般而言k的取值为10,常用的还有5、20等
自助法问题引出:我们希望评估的是用D训练出来的模型,但是留出法和交叉验证法中,由于保留了一部分样本用于测试,因此实际评估的模型所使用的训练集比D小,这必然会引入一些因训练样本规模不同而导致的估计偏差,为此提出自助法。
方法:它以自助采样(bootstrap sampling)为基础.给定包含m个样本的数据集D,我们对它进行采样产生数据集 D′:每次随机从D中挑选出一个样本,将其拷贝放入D′, 然后再将该样本放回初始数据集D中,使得该样本在下次采样时仍有可能被采样到;这个过程重复执行m次后,我们就得到可包含m个样本数据的数据集D′,这就是自助采样的结果.样本在m次采样中始终不被采到到概率为
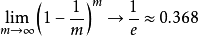
由此可知通过自助采样,初始数据集D中约有36.8%的样本未出现在采样数据集D′中。于是我们可将D′ 用作训练集,D∖D′用作测试集。
优缺点:自助法在数据集较小,难以有效划分训练/测试集时很有用,但是,自助法改变了初始数据集的分布,这会引入估计偏差,所以在数据量足够时,一般采用留出法和交叉验证法。4




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国