[科普中国]-靴襻法，自助法

靴襻法，自助法简介

靴襻法，自助法由Bradley Efron于1979年在《Annals of Statistics》上发表。是以自助采样(bootstrap sampling)为基础。给定包含m个样本的数据集D，我们对它进行采样产生数据集 D′：每次随机从D中挑选出一个样本，将其拷贝放入D′, 然后再将该样本放回初始数据集D中，使得该样本在下次采样时仍有可能被采样到；这个过程重复执行m次后，我们就得到可包含m个样本数据的数据集D′，这就是自助采样的结果.样本在m次采样中始终不被采到到概率为

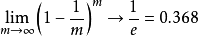
由此可知通过自助采样，初始数据集D中约有36.8%的样本未出现在采样数据集D′中。于是我们可将D′ 用作训练集，D∖D′用作测试集。

优缺点：自助法在数据集较小，难以有效划分训练/测试集时很有用，但是，自助法改变了初始数据集的分布，这会引入估计偏差，所以在数据量足够时，一般采用留出法和交叉验证法。1

抽样概述在统计学中，抽样（Sampling）是一种推论统计方法，它是指从目标总体（Population，或称为母体）中抽取一部分个体作为样本（Sample），通过观察样本的某一或某些属性，依据所获得的数据对总体的数量特征得出具有一定可靠性的估计判断，从而达到对总体的认识。

抽样过程抽样过程主要包括以下几个阶段：

定义总体（母体）

确定抽样框

确定抽样方法

决定样本量

实施抽样计划

抽样与数据收集

回顾抽样过程

抽样方法简单随机抽样（simple random sampling），也叫纯随机抽样。从总体N个单位中随机地抽取n个单位作为样本，使得每一个容量为样本都有相同的概率被抽中。特点是：每个样本单位被抽中的概率相等，样本的每个单位完全独立，彼此间无一定的关联性和排斥性。简单随机抽样是其它各种抽样形式的基础。通常只是在总体单位之间差异程度较小和数目较少时，才采用这种方法。2

系统抽样（systematic sampling），也称等距抽样。将总体中的所有单位按一定顺序排列，在规定的范围内随机地抽取一个单位作为初始单位，然后按事先规定好的规则确定其他样本单位。先从数字1到k之间随机抽取一个数字r作为初始单位，以后依次取r+k、r+2k……等单位。这种方法操作简便，可提高估计的精度。

分层抽样（stratified sampling）。将抽样单位按某种特征或某种规则划分为不同的层，然后从不同的层中独立、随机地抽取样本。从而保证样本的结构与总体的结构比较相近，从而提高估计的精度。

整群抽样（cluster sampling）。将总体中若干个单位合并为组，抽样时直接抽取群，然后对中选群中的所有单位全部实施调查。抽样时只需群的抽样框，可简化工作量，缺点是估计的精度较差。3

自助法在药物经济学评价中的应用在药物经济学研究中, 国外学者在利用可信区间法进行敏感度分析时，常用的方法有 Fieller 理论、 Taylor 公式和靴襻法(bootstrap method ) 分析。其中 Fieller 理论、Taylor 公式在计算成本 - 效果比的可信区间时要求成本和效果数据的分布满足正态分布，而实际上临床试验所得到的数据多数不服从正态分布，因此利用它们来计算增量成本 - 效果比的可信区间有一定的局限性。而 bootstrap 分析对数据的分布不作任何要求， 因而应用范围更广 。

Bootstrap 分析下面以样本均值方差的 bootstrap 分析来说明其基本思想：

首先假定 X ( 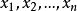) 是样本大小为 n 、来自于均值为μ且方差为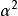的同一样本总体的一个抽样。假如用F表达样本总体的累积分布，则有 F ( x ) =Pr ( 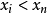) ，这意味着每一 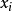是一具有累积分布 F 的随机变量，可简记为 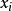～ F 。在实际中，经常假定样本总体服从高斯分布。此时，其样本均值的方差为：

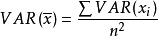
当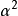未知时，由统计理论可知，样本方差的估计为

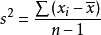
以上是对样本总体服从正态分布而言的，对于服从其他分布的样本总体，则很少有这样的解析解。样本均值方差估计的是具有同一总体分布 F 的各样本间的均值的变化。对于理想的情况， 假设有许多来自于同一总体的 F 的样本，则就不需要用如上所述的的估计式来估计方差, 因为此时可以直接从这许多的样本中求得均值, 然后由所得的均值求取方差。由于受到各种各样因素的影响，很难得到许多来自于同一分布的样本。然而，尽管不可能得到来自于同一分布 F 的总体的许多样本，但可以从近似于分布 F 的总体中获得样本。这就是 bootstrap 方法的基本思想，它用一个可重复抽样的分布 F 的估计代替未知的因而不能重复抽样的分布 F 。

计算步骤在药物经济学中, 将上述变量 “均值方差” 改为 “增量成本 - 效果比” 即可进行敏感度分析。计算步骤如下：① 产生与每组记录数相同个数的随机数， 按照随机数对各组进行有放回的随机抽样， 组成一个 boots 样本； ② 对该样本进行增量成本效果分析, 得到一个增量成本效果值；③ 重复产生 boots 样本，并计算增量值，循环 n 次( 一般 n>250 次) ；④对 n 个增量成本值进行排序，得到 5% 下限值和 95% 上限值。

应用实例本研究运用 bootstrap 分析对两种三联疗法治疗幽门螺杆菌( HP ) 感染的消化性溃疡方案进行药物经济学评价。

4治疗方案的选择：根据我院临床实际治疗抗 HP 感染的消化性溃疡情况，并参考有关文献， 分别选择以胶体铋( CBS )为基础的方案( BMA 三联疗法)和以质子泵抑制剂( PPI )为基础的方案( LMC 三联疗法) 。

病例选择： 选择经采用 Giemsa 染色法, 尿素酶试验、13 C 或 14 C- 尿素呼吸试验等检测HP 阳性的消化性溃疡门诊患者 186 例，其中十二指肠溃疡 155 例， 胃溃疡 31 例；年龄26～ 70 岁，平均 41 岁； 溃疡直径 5～ 20 mm ，数目 ≤2个，1 周内未接受铋剂和抗生素治疗，未服用非甾类抗炎药或皮质激素，排除复合性溃疡、 幽门梗阻、 活动性出血和心、 肺、 肝、 肾功能损害。186 例随机分成两组： A 组 96 例，男 70 例，女 26例，平均年龄( 42± 8 ) 岁；B 组 90 例， 男 62 例，女 28 例，平均年龄(40± 8 ) 岁。两组患者临床主要症状( 疼痛、 反酸、 烧心、 嗳气、 腹胀等) 比较差异无统计学意义。停药 4 周后复查胃镜,观察溃疡愈合情况, 重复检查 HP 。

检测方法及判断：两种方案在对 HP 的检测及判断方面基本相同, 其检测方法采用 Giemsa 染色法、尿素酶试验、13 C 或 14 C- 尿素呼吸试验等，几种检测方法均具有准确性。在HP 阳性及阴性的判断上也以 2 项检测方法具有相同的结果为准。

治疗方法： A 组( 采用 BMA 三联疗法) ：枸橼酸铋钾片( 德诺) 240 mg 、 阿莫西林片 500 mg 、 甲硝唑片 400 mg , 均每日2 次, 连用 2 周。 B 组( 采用 LMC 三联疗法) ：兰索拉唑 30 mg ，甲硝唑 400 mg ，克拉霉素 500 mg，均每日 2 次，连用 1 周。

成本确定：为使分析结果具有一定的参考意义， 所有费用均按 2004 年我院的实际价格计算。检验成本：Giemsa 染色法 20 元 / 次，快速尿素酶试验 20元 /次，H13 C 或 14 C- 尿素呼吸试验检测130 元 / 次，每位受试者按实际检测次数计算检验成本。药物成本：A 组单日成本 12.49 元，疗程 14 d ；B 组单日成本 77.48 元，疗程 7 d 。其他费用： 按实际发生计算。

效果确定：溃疡愈合标准按胃镜常规评定标准判定，HP 根除以两项检查均为阴性为判断标准， 如溃疡愈合、 HP根除则为有效，否则为无效。 A 组有效率为 87.5% ，B 组有效率为 92.2% 。

成本 - 效果比分析： 成本 - 效果比分析的目的在于通过分析寻找达到某一治疗效果时成本最低的治疗方案， 通常采用成本( C ) 与效果( E ) 比值法，其可将成本与效果两者有机地联系在一起， 它是采用单位效果所花费的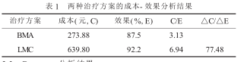成本来表示的，一般比值越低, 该方案的实施就越有益。在对不同治疗方案比较时，有的方案可能花费的费用成本很多，而且产生的效果也很好( 但有时也会出现相反的结果) ， 而增加效果则需要增加病人的支出， 因此就要考虑每增加一个效果单位所花费的成本， 即增量成本 / 效果( △C/△E ) 比， 它代表一个方案成本 -效果与另一个方案比较而得到的结果, 以成本较低一组作为参照，另一方案与之对比而得到 △C/△E 。两种根除 HP 治疗方案的成本 - 效果分析见表。