[科普中国]-混沌同步控制

混沌作为一种复杂的非线性运动行为，在物理学、气象学、电子学、信息学和经济学等领域得到了广泛的研究。其中为了利用混沌而展开的应用研究越来越引起人们的重视，并成为混沌研究的前沿课题和发展方向之一。1990年，美国海军实验室的L. M.Pecora和T. L. Carrol提出混沌自同步方法， 首次利用驱动-响应法实现了两个混沌系统同步，从而拉开了混沌同步方法研究与应用的序幕。

混沌同步，从总体上说，属于混沌控制的范畴。但由于混沌自身的特点，同步方法不完全和传统的以抑制混沌为主的控制方法相同。传统的混沌控制一般是将系统稳定在不稳定的周期轨道上，混沌同步则是实现两个系统的混沌状态的完全重构。

考虑如下两个非线性动力系统

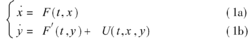
其中x , y∈ R分别为系统的状态变量。F，F‘为非线性映射，U为同步控制量。如果存在

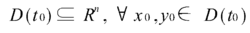
有

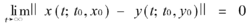
成立，则系统(1b)和系统(1a)同步。称系统(1a)为驱动系统，系统(1b)为响应系统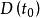， 为同步区域。如果F= F′，则称为自同步。该定义不仅适于混沌同步，而且也适于非混沌同步，还可拓广至超混沌同步。

令e=x-y为误差向量，则同步误差系统：

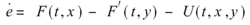
相应地，由误差系统在原点处的稳定性，可得到系统同步稳定性原理。在混沌同步中,目前主要根据Lyapunov 稳定性原理和由L. M. Pecora 和T.L.Carrol提出的条件Lyapunov指数判据来判断同步稳定性。

混沌同步，从总体上说，属于混沌控制的范畴。但由于混沌自身的特点，同步方法不完全和传统的以抑制混沌为主的控制方法相同。传统的混沌控制一般是将系统稳定在不稳定的周期轨道上，混沌同步则是实现两个系统的混沌状态的完全重构1。

Pecora和Carroll针对可分的混沌系统

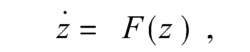
将其状态变量分解为u和v两部分，其中

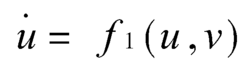
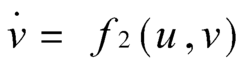
这样就得到驱动-响应总的动力学系统：

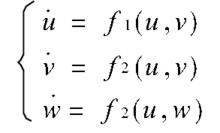
式中u为驱动变量。令e=v-w，则得到系统自同步的误差系统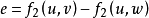 。可用前面的判据来判别同步的稳定性，即只有当响应系统的所有条件Lyapunov 指数都是负值时，才能达到响应系统和驱动系统的同步。

该方法的主要特点是：两个非线性动力学系统之间存在着驱动与响应（Drive-Response）关系。响应系统行为取决于驱动系统，而驱动系统的行为与响应系统的行为无关。对于某些实际的非线性系统，由于物理本质或天然特性等原因，系统无法分解，这时，驱动-响应同步方法也就无能为力了。

主动-被动的同步方法由L.Kocarev和V.Parlitoz于1995年提出。假设一个自治非线性动力学系统为

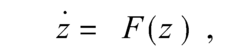
将它改为非自治形式：

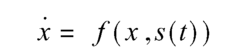
复制一个相同的系统：

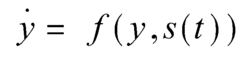
变量差e=x-y的微分方程：

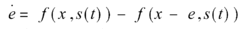
显然，该式在e= 0处有一稳定的不动点，故存在一个稳定的同步态：x = y 。

应用Lyapunov函数或线性稳定性分析方法（在e为小值情况下），可证明：只要非自治的条件Lyapunov指数都是负值，由x和y所表示的两个混沌系统就能实现同步。

因y式不被驱动时，即s(t)=0，它是一个趋向不动点的被动系统（或称无源系统），因此称该同步方法为主动-被动（或有源-无源）同步方法。

该方法的优点是可以不受任何限制地选择驱动信号的函数，因此，十分灵活且具有较大的普遍性和实用性，且把驱动-响应同步法作为特例包括在内。在很多情况下，s(t)可以是一般函数，它不仅依赖于系统的状态x而且可以与信息信号i(t)有关，即s(t)=h(x,i) 或s=h(x,i,s)。该特点使主动-被动同步方法特别适合于保密通信方面的应用。

耦合同步法由A.V.Gaponov-Grekhov在80年代研究流体湍流时提出。1994年，美国学者Roy与Thornburg及日本学Sugawara，Tachikawa等人分别独立地从两个混沌激光系统的实验中观察到了同步现象。大量研究表明：相互耦合的混沌系统在一定条件下，可实现混沌同步。Kapitaniak和Chua等人用相互耦合的方法，使两个Chua 氏电路达到了混沌同步。Chua氏电路的状态方程可简写为：

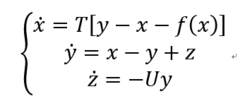
其中

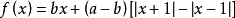
考虑下列两个线性相互耦合的Chua氏电路：

电路1：

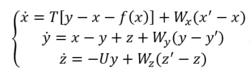
电路2：

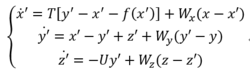
当参数T=10.0，U=14.87，a=-1.27，b= 0.65时，Chua式表示的蔡氏电路处于混沌态，可以证明，耦合系数取值为

（1）

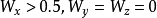
（2）

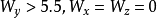
（3）

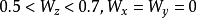
时，电路1和电路2能实现混沌同步相互耦合的非线性系统，动力学行为十分复杂，到目前为止尚无一般的普适性理论。但相互耦合的非线性系统在自然界中普遍存在，因此，对这种同步方法的理论和实验研究具有重要意义。

1993年，K.Pyragas 提出了一种非线性连续混沌系统的控制方法。后来这一思想被用来研究两个混沌系统的同步问题，其同步原理如图所示：

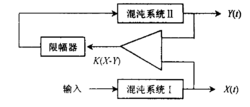
由混沌系统Ⅰ和混沌系统Ⅱ组成的同步系统方程为：

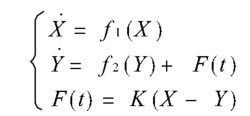
F(t)与两个系统的状态变量的差值成正比，它作为小微扰信号反馈到系统Ⅱ中。只要选取适当的系数K，系统Ⅰ和混沌系统Ⅱ就可以达到同步。

连续变量反馈同步法简单，易于实现，具有一定的实用价值。根据具体系统，可以灵活采用单变量、多变量甚至所有系统变量反馈微扰。研究表明：反馈变量的最小数目应等于无微扰系统的正的Lyapunov指数的数目，而且多变量反馈比单变量反馈更为有效，收敛的速度更快。

分别用驱动-响应同步，相互耦合同步、反馈微扰同步、自适应控制同步和脉冲同步方法，对Lorenz混沌系统的同步建立时间和对参数变化的敏感性进行仿真，结果见表：

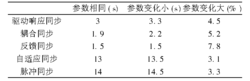
Lorenz电路反馈微扰同步对参数的变化的鲁棒性最好，同步建立最快，系统安全性好。而自适应同步和脉冲同步的同步建立时间比较长，对参数的变化的鲁棒性差，采用的方法相对较复杂，但安全性最好。从同步建立时间和对参数变化的鲁棒性来看，反馈微扰同步方法更优。