基本概念
加法器是实现两个二进制数相加运算的基本单元电路。8位加法器就是实现两个 8位二进制相加,其结果的范围应该在00000000到111111110之间,八位二进制数换算成三位十进制数最大为255,也就是说要输入两个000到255之间的数。
设计思路8位二进制加法器,它的功能主要是实现两个8位二进制数的相加,其结果的范围应该在00000000到111111110之间,八位二进制数换算成三位十进制数最大为255,也就是说要输入两个000到255之间的数。要实现它们的相加,下面有三种方案。
方案一当输入两个三位十进制数时,由于在数字电路中运算所用到的是二进制数,因此我们必须首先将十进制数转换为二进制数,于是一个问题出现了,那就是,我们如何实现十进制数到二进制数的转换,通过查阅相关资料,我们发现二-十进制编码器(也叫8421BCD码编码器,在实际中通常指74LS147)可以实现从十进制数到二进制数的转换,于是我们通过二-十进制编码器来实现上述的转换。由于二-十进制编码器可以实现一位十进制数到四位二进制数的转换,而题目中的是两个三位十进制数,因此我们就需要用到6个二-十进制编码器,分别将三位十进制数的个位、十位、百位转换为其各自对应的8421BCD码,于是我们得到了两个十二位的8421BCD码。于是如何实现两个三位十进制数的相加这个问题就变成了如何实现两个十二位的8421BCD码相加这个新问题。那么,如何实现呢?我们想到了加法器,常用的加法器74LS283能够实现四位二进制数的相加,于是我们就要将74LS283进行串联,实现十二位数的相加,但加法器74LS283的进位是逢16进1,而这两个十二位的8421BCD码相加时的进位是逢10进1,那么就要对加法器74LS283的二进制和数进行修正,即加上一个6(0110),让其产生一个进位。于是把大于9的项画在卡诺图里,另外考虑到若相加产生进位,则同样出现大于9的情况。综合考虑,得到修正和数的条件,用与非门和与门来实现,得到了一个新的加法器,它可以实现逢10进1这个条件。将这两个十二位的8421BCD码分别接到三个新的加法器的输入端,得到一个新的十二位的8421BCD码。由于结果要得到一个三位十进制数,因此再将这个十二位的8421BCD码通过三个7447七段显示译码器转换为一个三位十进制数,通过数码管将它显示出来,即为所求的结果。
方案二当输入的不是三位十进制数而是八位二进制数时,我们如何实现它们的相加呢?我们知道,超前进位并行加法器74LS283可以实现四位二进制数的相加,于是,我们需要两个74LS283进行串联,这样我们就得到一个新的九位二进制数,其范围在000到510之间。那么我们如何实现从九位二进制数到三位十进制数的转换呢?我们就想到了数码转换器,通过74185芯片来实现字码的转换。这样,就得到了一个新的十二位8421BCD码,再通过7447七段数码显示译码器来实现8421BCD码到三位十进制数的转换,最后通过数码管显示出来,得到的就是所要求的的八位二进制数的和。
方案三通过上述两种思路,我们会要进一步想到,能不能同时实现八位二进制数和三位十进制数的相加呢?那么我们可以对上述的思路加以扩展,假设输入的是三位十进制数,我们可以设法将其转换为BCD码,再通过加法器输出。这样,我们既可以输入三位十进制数,也可以输入八位二进制数。那么三位十进制数如何转换为八位二进制数呢?我们想到了二-十进制编码器,一个二-十进制编码器可以实现一位十进制数到四位二进制数的转换,那么我们就可以将一个二-十进制编码器和一些与非门组成一个新的二-十进制编码器来实现这个三位十进制数的十位到8421BCD码的转换;同理,三位十进制数的百位也可以这样转换。于是三位十进制数就转换到了八位二进制数,接着,我们就可以用第二种思路来实现八位二进制数的相加。
8位加法器的实现通过以上三种思路,经过分析验证,在实践论证中我们发现,由于第一种思路所用的元件少,且个位、十位、百位各自对称,因此在连接上方便可行,不易出错。同时由于原理清晰,一旦出现错误,我们可以尽快发现问题并加以改正。在论证第二种思路时,我们发现,在使用译码器时,由于使用的是4线-16线译码器74LS154,因此它有16个出线端。而我们要实现九位二进制数到十二位BCD码的转换,就要有512个出线端,也就是512除以16,即32个译码器。由于所用到的译码器数量冗长,在连接上容易出错。因此并不采纳。同理,第三种思路也是如此。
系统框图当输入为十进制数时:
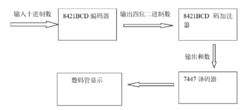
当输入为二进制数时:
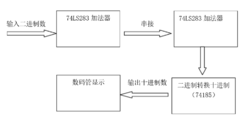
原理当输入十进制数的时候,8421BCD码编码器先开始工作,编码器先将十进制数转换成四位二进制数,输出的四位二进制数直接到达8421BCD码加法器的输入端,我们可以使用71LS185加法器构成的一位8421BCD码的加法器,8421BCD码是用4位二进制数表示1位十进制数,4位二进制数内部为二进制,8421BCD码之间是十进制,即逢十进一。而四位二进制加法器是按四位二进制数进行运算,即逢十六进一。二者进位关系不同。当四位二进制数加法器74LS283完成这个加法运算时,要用两片74LS283。第一片完成加法运算,第二片完成修正运算。8421BCD码加法器工作时,8421BCD码的加法运算为十进制运算,而当和数大于9时,8421BCD码就产生进位,而此时十六进制则不一定产生进位,因此需要对二进制和数进行修正,即加上6(0110),让其产生一个进位。当和数小于等于9时,则不需要修正或者说加上0。因此我们可以通过三个8421BCD码加法器的相连组成一个三位串行进位并行加法器,这样通过低位向高位产生进位进行十进制的加法运算,最后通过连接数码管显示所得的结果。当输入二进制数的时候,两个串接的74LS283四位加法器进行加法运算,产生的八位二进制数通过集成芯片转换成三位十进制数,最后通过数码管显示。
基于FPGA的8位加法器原理图输入方式原理图输入,这是一种最直接的设计输入方式,它使用软件系统提供的器件库及各种符号和连线画出设计电路的原理图,形成图形输入文件。这种方式大多用在设计者对系统及各部分电路很熟悉或系统对设计特性要求较高的场合。优点是容易实现仿真,便于信号的观察和电路的调整1。
由于MAX+PLUSII软件的宏函数库种有8位加法器的元件,这样我们只要调用出这个8fadd元件,再加上输入、输出即可。整体设计如图:
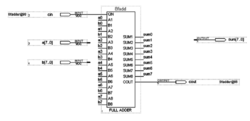
文本输入法文本输入是指采用硬件描述语言进行电路设计的方式。硬件描述语言有普通硬件描述语言和行为描述语言,它们用文本方式描述设计和输入。行为描述语言是目前常用的高层硬件描述语言,有VHDL和Verilog HDL等,这里用VHDL,它具有很强的逻辑描述和仿真功能,可实现与工艺无关的编程与设计,输入效率高,在不同的设计输入库之间转换也非常方便。运用VHDL等硬件描述语言进行设计已是当前的趋势。8位加法器用文本输入法输入也非常简单方便。下面是8位加法器的VHDL源程序:
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_UNSIGNED.A L L ;
ENTITY adder8 IS
PORT(CIN:IN INTEGER RANGE 0 TO 1;
A:IN INTEGER RANGE 0 TO 255;
B:IN INTEGER RANGE 0 TO 255;
SUM:OUT INTEGER RANGE 0 TO 255;
COUT:OUT INTEGER RANGE 0 TO1);
END adder8;
ARCHITECTURE a OF adder8 IS
SIGNAL SINT:INTEGER RANGE 0 TO 511;
BEGIN
SINT




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国