[科普中国]-低速流

定义

低速流是指可以忽略流体密度变化影响的流动。一般指马赫数小于0.3的流动。1

密度与马赫数的关系真实流体都具有程度不同的可压缩性，但液体的压缩性很小，流动中的压强变化不足以引起明显的密度变化（水下爆炸、水击等情况除外），因而液体流动一般都属不可压缩流动。气体流动中的密度变化可按欧拉方程分析：

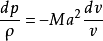
式中Ma是马赫数，ρ、v分别是密度和速度。若Ma很小，则密度变化可以忽略，属不可压缩流动范畴 。若Ma不很小，如大于0.3，则密度变化不可忽略，属可压缩流动。在不可压缩流动中，流动参数通常仅为速度和压强；但在可压缩流动中，还须增加密度，并伴随温度。变量增加了，控制方程的数目和求解的复杂性也增加了。可压缩流动按马赫数大小可分为亚声速流动（Ma=0.3～0.8左右）、跨声速流动（Ma=0.8～1.2左右）、超声速流动(Ma=1.2～5.0左右)和高超声速流动（Ma>5.0）。高速飞行器和航天器的飞行马赫数大多远超过0.3 ，其绕流问题都必须按可压缩流动的理论处理。

近三十年来，随着高速飞行、喷气发动机、火箭、空间飞行、弹道学、燃烧学、燃气涡轮、冲压喷气发动机、传热学等方面的发展，可压缩流动理论的研究取得了巨大进展，已成为一个重要的科学领域。

不可压缩流不可压缩流是密度不发生变化的流体运动。而定常是指流体和时间无关。确切地说， 是流体在一个大时间段后某一时刻的状态或者趋于稳定的状态。为了实用的目的，假设流体在流动时为不可压缩流体。在低速下，这大体上是对的;但是，甚至对于液体，速度的急剧变化也会产生压缩或者膨胀。通常，液体在重力作用下流动，因而在一个开放容器中它占据着较低的部分。这一性质是液体独具的特性。相反，气体可压缩地流动，不管气体和空间的初始容积有多大，它都占据整个限制它的任何封闭空间。这一性质是气体所特有的。像液体的情况一样，对气体的缓慢流动采用不可压缩的假设可以获得良好的近似结果。特别地， 它的研究对人们认识和控制湍流至关重要。描述这种流体的控制方程主要有不可压缩Navier–Stokes方程，还有不可压缩Stokes方程以及Stokes特征值问题。2

分析不可压缩流常常以对无粘性或“完全”流体的解附加上流体粘性效应的方法加以分析。像均匀流、源、汇和涡这样一些简单的流动，可以用确定流动速度的数学表达式表示出来。这些解可以叠加起来，以表达像在空气中运动的机翼或在水中运动的船体这样一些实际的复杂无粘性流。结果得到流场中所有点上的速度的大小和方向的数学表达式。然后通过伯努利方程，可以把流动中某一点上的压力(P)与速度(v)联系起来。这样，由压力引起而作用在边界上的力就可以计算出来。然后，余下的问题就是确定粘性如何影响流场和压力分布，以及流体摩擦引起的平行于边界的附加力。在不可压缩流这一领域中，粘性起着重要的作用，因为它决定了靠近流动边界的流体(边界层)的行为，以及流体不沿着边界流动的区域(分离区)中的流体行为。雷诺数，即流体中惯性力和粘性力的无量纲比值，给出流动特性的一个量度，它对于把实验数据和理论联系起来是十分有用的。3