[科普中国]-切换布尔网

定义

布尔切换网的动力学表示如下

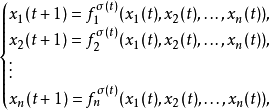
其中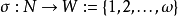 为切换信号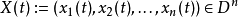， 为逻辑状态，

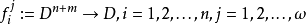为逻辑函数。

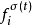
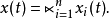应用逻辑变量的向量形式并令假设的逻辑矩阵为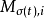

利用半张量积理论，可以将上述动态方程组转化为

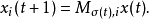
将上式的每个子式乘积可以得到动态方程组的代数表达式如下

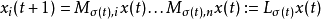其中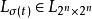 为系统的状态转移矩阵，并且有 。

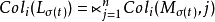多模态切换现象成因在实际基因调控网络的动态行为中，多模态切换时常出现。这种多模态切换现象主要由以下下方而的因素所导致:

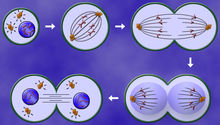
(1)系统自身所同有的属性.例如，真核细胞的生长和分裂由四个模态构成，每一个模态都由某些离散事件激发所引起(参见图1).在细胞的分化模型中，由于Delta-Notch蛋自的相互作用，系统的动态演化也呈现多模态切换；.

(2)试图重构给定网络的外部干扰或控制.D. Laschov等在文献1中指出，通过将控制输入编码成切换信号，一个布尔控制网络可转化为布尔切换系统；

(3)网络进化的异步行为也会产生多模态切换.文献2指出，通过排列所有可能的布尔函数，一个确定性异步布尔网络可以转化为切换布尔网络。

研究难点(1)切换布尔网络的状态与控制取值只有有限个点，状态空间是一个有限集，人们很难定义一个公共的距离来衡量所有布尔网络的收敛特性；

(2)切换布尔网络是一个切换信号和离散逻辑状态并存的混杂系统，每个子模态都是由布尔差分方程所确定的强非线性系统由于用米处理一般切换系统的工具大都只适用于普通的加法和乘法运算，这就使得它们很难被用来处理切换布尔网络中的逻辑加和逻辑乘等运算；

(3)布尔网络的函数的概念尚未被提出，因此依赖于Lyapunov函数的共同Lyapunov函数法和多重Lyapunov函数法无法直接用来研究切换布尔网络。

研究成果李海涛、孙玉振等人建立了一套采用矩阵半张量积理论框架研究切换布尔网络的分析与控制问题的方法，主要研究了该类系统的能控性、稳定性等基本分析问题，并基于此研究系统的镇定控制、干扰解耦控制、最优控制等控制问题，建立一套适用于切换布尔网络的分析与控制方法3456。

基于矩阵半张量积的研究方法同时把所得到的研究结果应用于细胞调控网络的分析与控制、组合电路的故障诊断和有限域网络的趋同分析中。