[科普中国]-球密堆积

构成晶体的粒子、原子和离子等可视为具有一定体积的圆球。对于金属晶体和离子晶体，常常可以将其结构看作是这些圆球以尽可能紧密的方式堆积在一起的。

简介等径圆球的堆积有最密堆积和其他形式的堆积，最密堆积的结构可以从密堆积层来了解。密堆积层的结构只有一种形式，如下图：

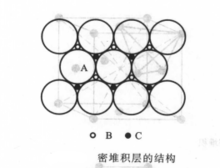
A表示球心位置，B表示顶点向上三角形空隙中心位置，C表示顶点向下三角形空隙中心位置。在层中每个球和周围6个球接触，即配位数为6，在密堆积层中，每个球周围有6个三角形空隙，每个空隙由三个球组成。这些三角形空隙分为两类，它们的顶点朝向相反。

由密堆积层进行堆积时。若采用最密堆积的方式，必须是堆积层中的每个球正好对准相邻一层中的一类三角形空隙，即每一个球都同时和相邻一层的3个球相接触。按照这种方式将密堆积层堆积起来，才能形成最密堆积的空间结构。按照这个原则作最密堆积寸，各密堆积层的相对位置实质上只有三种情况，这可把各层球心所处的相对位置投影到上图中标明的A、B、C三种位置上来加以区分。1

堆积方式常见的最密堆积结构有两种，即立方最密堆积和六方最密堆积。下面主要讨论立方最密堆积和六方最密堆积方式，简要介绍圆球的立方体心密堆积和简单立方堆积。

1、立方最密堆积

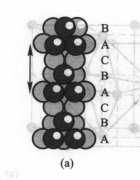
将密堆积的相对位置按照ABCABC ABC…方式作最密堆积，这时重复的周期为3层，如图（a）所示，由于从这种最密堆积方式中可划出面心立方品胞，故称为立方最密堆积，记为A1型堆积。

2、六方最密堆积

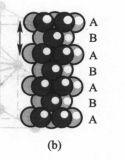
将密堆积的相对位置按照ABABAB…方式作最密堆积，其重复周期为两层，如图（b）所示。由于这种堆积方式可划出六方晶胞，故称为六方最密堆积，记为A3型堆积。除上述两种最密堆积外，最密堆积方式还有ABAC…和ABABCBCAC等形式。

3、立方体心密堆积

立方体心密堆积，记为A2型堆积。但这种密堆积并不是最密堆积，堆积系数为0.6802。立方体心密堆积结构中，每个圆球均有8个最近的配位球，处在立方体的8个顶点上；另外还有6个稍远一点的配位球，所以有效配位数可看作8和14之间。

4、简单立方堆积 ·

简单立方堆积是密堆积程度更差的一种圆球堆积方式，它是8个圆球堆成一个立方体，这种堆积方式的堆积系数是0.5236，配位数是6，只形成立方体空隙。

堆积特点（1）各种形式的最密堆积中，每个球的配位数均为12，即每个球有12个最相近邻的球，这12个球中，有6个球与中心球处于同一密堆积层，另外6个球分别位于与中心球相邻的上下密堆积中。

（2）有相同的堆积密度，其堆积系数即空间利用率均为0.7405。堆积系数即球体积与整个堆积体积之比，可按下图中的立方最密堆积的一个晶胞进行计算。

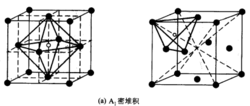
设球的半径为R，晶胞边长为a，面对角线长为4R，它等于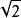 a，所以

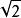a=4R/ =2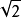 R，晶胞体积V晶胞=a3=16 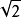R3。

晶胞内4个圆球的总体积V球=4×（4πR3/3）=16πR3/3。

堆积系数=V球/V晶胞=0.7405。

（3）在各种最密堆积中，球间的空隙类型、数目和大小也相同。由N个半径为尺的球组成的最密堆积中，平均有2N个四面体空隙，可容纳半径为0.225R的小球；还有N个八面体空隙，可容纳半径为0.414R的小球。

举例金属单质的结构若将金属键看作原子间各向同性的相互作用，金属原子在晶体中总是趋向于最紧密的方式堆积，即按立方最密堆积A1或六方最密堆积A3进行排列。

例如属于A1型的金属晶体有Al、Sr、Ni、Pd、Pt、Cu、Ag、Au、Pb等；属于A3型的Be、Mg、Sc、Ti、Co、Zn、Cd等；属于A2型的有Li、Na、K、Rb、Cs、V、Nb、Ta、Cr、Mo、W等。由于温度和压力等外界条件的改变，有些金属可以有不同的构型，如α-Fe为A2型，γ-Fe为A1型。

离子晶体的堆积方式许多离子晶体的结构可以按密堆积结构了解其特征，一般负离子半径较大，可把负离子看作等径圆球进行密堆积，而正离子有序地填人负离子所形成的某种空隙之中。根据离子晶体的组成，空隙的占有分数不同，有的能将某种空隙全部填满，有的只是部分填人。

下面列举几种离子晶体的堆积方式：

1、在NaCI结构中，Cl-离子以A1型密堆积，Na+离子占据全部八面体空隙。若以密堆积层的形式描述，Cl-离子堆积层的相对位置用A、B、C表示，小的正离子Na+在层中的相对位置用a、b、c表示，沿堆积层的法线方向NaCI中正、负离子的堆积周期∣AcBaCb∣。

2、ZnS的结构可看作S2-的最密堆积，Zn2+填充在一半四面体空隙之中，填隙时互相间隔开。使填隙四面体不会出现共面连接或共边连接。在立方ZnS结构中，S2-采取立方最密堆积，按密堆积层的形式描述，其结构可表达为∣AaBbCc∣。在六方ZnS结构中，S2-采取六方最密堆积，密堆积层堆积表示式∣AaBb∣

3、CaF2的晶体结构可看作F-的简单立方堆积，Ca2+填人立方体空隙中，由于Ca2+数目比F-少一倍，所以有一半空隙是空的，只有一半的立方体空隙填Ca2+，Ca2+与空位交替地在空间间隔排列。CaF2晶体也可看作Ca2+的立方最密堆积，F-填在全部的四面体空隙中。

本词条内容贡献者为:

代祥光 - 副教授 - 西南大学电子信息工程学院