[科普中国]-立方型状态方程

方程类型Van der Waals 状态方程

1873年J.D. Van der Waals提出了第一个适用于真实气体的状态方程，可写为：

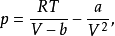其中a,b是各种物质特有的常数，与其临界参数有关。

Van der Waals方程是最简单的立方型状态方程。该方程能定量地描述流体的P-V-T关系，能够同时描述气、液两相的性质。虽然精确度不高，但还是特别值得关注，因为它建立方程的推理方法对立方型方程、对比态原理以及后来与之类似的状态方程的开发有着巨大的贡献。1

Redlich Kwong 方程该方程由Redlich和Kwong于1949年提出，简称为RK方程，其形式如下：

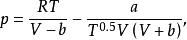其中a,b为RK常数，与流体的特性有关。

RK方程与Van der Waals方程的区别仅在于压力修正项的形式不同。1

Soave Redlich Kwong方程SRK方程，其形式为：

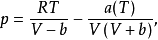
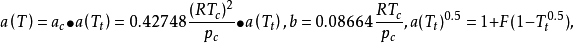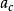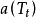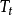其中 是临界参数有关的常数； 是对比温度 的函数，其中的参数F可由纯物质的饱和蒸气压和液体的密度数据关联得到，对于非极性或弱极性物质，F可以通过下式进行计算：

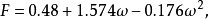其中ω为偏心因子。

与RK方程相比，SRK方程显示出很大的优越性，特别是用它来计算纯烃和烃类混合物系统的气液平衡具有较高的精度，该方程在烃应用方面做出了很大的贡献。1

Peng Robinson 方程RK和SRK方程有一个共同的不足，就是预测液相摩尔体积时精度相当差。为了弥补这一不足，Peng和Robinson 于1976年提出了如下形式的状态方程：

。

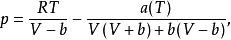
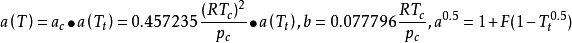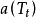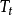PR方程中的 是对比温度 的函数，其中的参数F可由纯物质的饱和蒸气压与饱和液体的密度数据关联得到，对于非极性或弱极性物质，F亦可以通过下式计算：

。

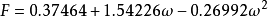PR方程的临界压缩因子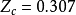 ，该值比RK方程的0.333有明显改进，但仍偏离真实流体的数值。PR方程计算饱和蒸气压、饱和液体密度和气液平衡的准确度均高于SRK方程。值得指出的是，SRK方程和PR方程在预测流体的蒸气压时显示出突出的优势，其主要原因在于温度函数a(T)的表达式。1

Patel Teja 方程1982年，由Patel 和Teja导出了Patel Teja方程，其形式为：

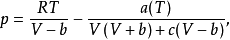
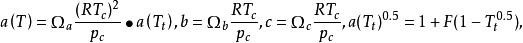其中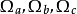 的计算方法如下：

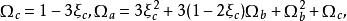
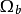是下列方程的最小正根：。

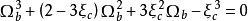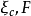这两个参数是由纯物质的饱和蒸气压和饱和密度数据关联得到的，对非极性或弱极性物质也可由以下两个式子求得：1

。

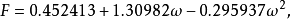
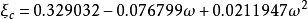通用形式一般式立方型状态方程可归纳为如下形式：

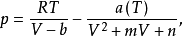其中，对于不同的立方型状态方程，m,n取不同的值，并且满足如下关系：

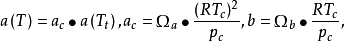
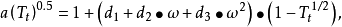其中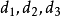 为关联常数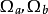， 均为与临界性质有关的参数。1

各方程对应参数值（1）Van der Waals方程：m=0，n=0， ；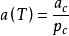

（2）Redlich Kwong 方程：m=b，n=0， ；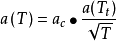

（3）Soave Redlich Kwong方程：m=b，n=0， ；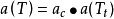

（4）Peng Robinson 方程：m=2b， ， ；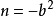

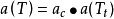（5）Patel Teja 方程：m=b+c，n=-bc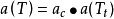， 。1

方程的求解虽然立方型状态方程可以用解析法求解三个体积根，但工程计算通常采用迭代法。下面具体介绍迭代过程，以Peng Robinson 方程为例进行讨论。

已知：

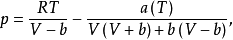
为便于迭代，将上式恒等变形，得到：

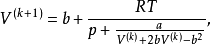
利用上式进行迭代计算时，体积根的初值设定方法为：

（1）对于气相，取初值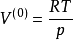 ，即以理想气体作为初值；

（2）对于液相，取初值 。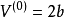

计算出初值后代入上式右端，在迭代收敛后即可得到气相摩尔体积或液相摩尔体积。1

应用立方型状态方程的应用：

（1）用一个EOS即可精确地代表相当广泛范围内的实验数据，借此可精确计算所需的数据；

（2）EOS具有多功能性，除了pVT性质之外，还可用最少量的数据计算流体的其他热力学函数、纯物质的饱和蒸气压、混合物的气一液相平衡、液一液相平衡．尤其是高压下的相平衡计算；

（3）在相平衡计算中用一个EOS可进行两相、三相的平衡数据计算，状态方程中的混合规则与相互作用参数对各相使用同一形式或同一数值，计算过程简捷、方便。1