[科普中国]-吉布斯自由能变

按照国际纯粹与应用化学联合会( IUPAC)的定义，吉布斯自由能或吉布斯函数是焓(H)减去热力学温度(T)和熵(S)的乘积，即G=H-TS，常称为自由能或自由焓。其 SI 单位为焦耳(J)。与其他热力学函数一样，G也具有状态函数的属性。由于H绝对值未知故G的绝对值也是不可知的，但其变化量即ΔG只决定于系统的始态和终态，而与变化的具体途径无关。吉布斯自由能具有广泛的功能特性，如在等温、等压条件下可作为反应自发进行方向的判据，还具有狭义化学势、最大非膨胀功和狭义表面自由能等功能。这些功能特性往往都是以其改变量ΔG来体现的。1

简介吉布斯自由能G是物理化学中非常重要、应用非常广泛的一个热力学状态函数。它的绝对值的大小我们没有办法得知，而其改变量△G却可以通过一定方法进行计算，且△G的计算在一定程度上显得更为重要。因为吉布斯自由能G虽然是在热力学第一定律和第二定律的基础上，在定温定压条件下经过一定的热力学推导而定义的一个热力学状态函数，但并不是只有在定温定压条件下的系统才有吉布斯自由能，也不是只有在定温定压下系统状态发生变化时才有吉布斯自由能变△G，而是在任意条件下，当系统处于一定状态时就有确定的吉布斯自由能G，当系统的状态发生改变时就有吉布斯自由能变△G的存在，无论是简单的状态变化过程，还是复杂的化学变化过程和相变化过程都是如此。我们知道，△G可用于判断定温定压下各种热力学过程自发进行的方向和限度，而在实际过程中常遇到的各种热力学过程往往是在定温定压条件下进行的。因此，虽然热力学判据较多，如熵判据，亥姆霍兹自由能判据等。而吉布斯自由能变△G作为判据更为有利和方便。2

单纯状态变化过程中的计算理想气体定温过程对于理想气体状态变化，可根据热力学的基本公式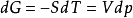 ，定温过程dT=0，则有 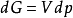，积分可得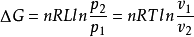 ，即根据此式可直接计算△G，再根据△G的正负来判断过程的自发性。

理想气体混合过程若热力学系统是由两种或两种以上理想气体混和而成，且每种气体单独存在时的温度和压力相等且等于混和气体的温度和压力，则该混和过程中吉布斯自由能变可根据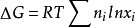 进行计算，式中ni为系统中i组分的物质的量，xi为系统中i组分在混和气体中的物质的量分数，T为系统的温度，R为气体常数。

非理想气体系统定温过程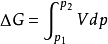 对于非理想气体系统，△G的计算，一方面可以用，只要找出系统中V与P之间的函数关系式，将V用含P的关系式代替代入公式，积分求解即可得△G。另一方面，可根据△G=△H一T△S。△H的 利用上式便可方便求出过程的△G，进而根据△G的正负判断过程的自发性。2

相变化过程中的计算相变化过程可分为两种情况。一种是系统在发生相变化的过程中始态和终态的两个相始终是平衡的，即系统发生的是可逆相变化，另一种情况是系统在发生相变化的过程中始态和终态的两个相是不平衡的，即为不可逆相变化过程。系统发生相变化的方式不同，其吉布斯自由能变△G的计算方法也有所区别。

可逆相变过程中对于可逆相变化过程，由于它是在温度和压力一定的条件下进行的，由△G=△H一T△S，△H是可逆相变热，△S是可逆相变时的熵变。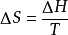 ，因此，可逆相变过程中吉布斯自由能变 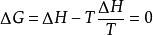。故当系统发生可逆相变化时，无需计算，△G=0，反过来，如果某一相变化过程中△G=0，则该系统所发,生的相变化一定为可逆相变。

不可逆相变过程中对于不可逆相变过程，直接计算该过程的△G是不可能的。但这并不意味着该过程的△G无法计算，因为我们总可以将不可逆相变过程设计为始态和终态与此不可逆相变过程相同的可逆过程，然后直接利用公式进行计算。2

反应方向判据若系统在等温、等压且不做非膨胀功的条件下，其变化值可以表示为-ΔG≥ 0或ΔG≤ 0，即自发变化总是朝着Gibbs自由能减少的方向进行，直至平衡为止。系统不可能发生ΔG> 0的变化。Gibbs自由能的变化值可作为等温、等压且不做非膨胀功条件下自发变化方向的判据。由于大多数反应都是在等温、等压条件下进行，与其他判据相比，Gibbs自由能判据更为常用。

对于任意化学反应，其变化方向可通过化学反应的等温方程式（van′t Hoff等温式）进行判断，即

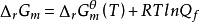或 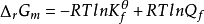（Qf表示反应系统的逸度商，Kθf为系统的热力学平衡常数）。通过比较Qf和Kθf数值的相对大小，即可获得ΔrGm 0的结果，并可以此判断化学变化的方向。

在理想气体混合物系统中，由于Qf= Qp，Kθf= Kθp，化学反应等温式可表示为：

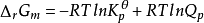
若Kθp> Qp，则ΔrGm

若Kθp= Qp，则ΔrGm= 0，表示系统已处于平衡状态；

若Kθp 0，表示对于给定反应式，反应不能向右自发进行。3

狭义表面自由能在表面物理化学的研究中，在指定各相应变量不变的情况下，每增加单位表面积时，系统热力学能或Gibbs自由能等热力学函数的增加值称为广义表面自由能。而狭义表面自由能是指，当以可逆方式形成新表面时，环境对系统所作的表面功变成了单位表面层分子的Gibbs自由能。

基于Gibbs自由能所具有的狭义表面自由能的性质，可以对很多实际系统进行分析。例如，在胶体分散系统中，其聚结过程是热力学的自发过程，即ΔG

选用高分子物质作为胶体系统的分散稳定剂时，当浓度和相对分子质量合适时，吸附在胶体颗粒表面的高分子物质可以降低胶体的表面能，有效避免颗粒聚集过程的发生，使胶体颗粒稳定。当高分子物质浓度较低时，不能将每个胶体颗粒包住，反而起到架桥作用，使颗粒间产生吸引作用，最终发生絮凝。因此，在很多实际体系中，如污水处理，高分子絮凝剂在加入量少时容易发生絮凝，而加入量多时可以起到保护胶体的作用。另外，利用分散制备法获得固体分散体系时，常加入表面活性剂来稳定胶体颗粒。表面活性剂的加入，不仅能降低表面张力，而且在胶体颗粒表面形成溶剂化膜或双层膜，达到降低胶体颗粒表面能的作用，使得胶体颗粒更稳定。3

吉布斯自由能的生物学意义从吉布斯自由能的物理意义可以了解其生物学意义，在可逆的等温等压过程中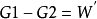 ，这表明，在等温等压过程中，系统吉布斯自由能的减少等于除去体积膨胀功以外，系统对外界所作的功。根据功能原理容易理解，系统的吉布斯自由能是指系统总能量中能作除膨胀功以外的其他有用功的那部分能量。由于生命体系中发生的绝大多数过程(化学反应过程、生理过程等等)都是在等温等压下进行的，因此，对生命体系而言，吉布斯自由能就是生命体系在等温等压条件下维持正常运转所需要的最小能量。那么，生命体系中的吉布斯自由能从何而来?它又是如何运转的呢?

众所周知，植物通过光合作用俘获光能，利用光能合成碳水化合物，碳水化合物在体内经过分解代谢逐渐放出能量，再用此能量驱动生命过程的进行。因此，碳水化合物分解放出的能量就是吉布斯自由能，而太阳则是生命体系吉布斯自由能的唯一来源。据计算，1mol葡萄糖完全氧化时放出的吉布斯自由能约为2879kJ，利用这个能量，动植物可以产生总量为38mol的高能化合物三磷酸腺苷(ATP)，这些ATP作为能量的货币再被用于维持细胞生存。

另一方面,，就吉布斯自由能的变化而言，如前所述，它可以作为判断等温等压过程能否自发进行的判据。由于生命体系内发生的过程大都是等温等压过程，因此，吉布斯自由能的这一功能对于生命过程也具有实际意义。在生命体系中，为了保证某一过程能够自发进行，常常进化出一些偶联反应，通过反应之间的偶联满足ΔG

系的呼吸代谢中，大量存在的葡萄糖和无机磷生成6-磷酸葡萄糖的反应，其ΔG= 17.1 kJ/mol。由于ΔG>

0，这一反应过程是不能自发进行的，但是，如果偶联一个三磷酸腺苷和水生成二磷酸腺苷与无机磷的反应,这一反应的ΔG= - 30.5 kJ/mol。两个反应偶联。总的吉布斯自由能变ΔG= 17.1+(- 30.5)= - 13.4(kJ/mol)

总之，吉布斯自由能对于生命体系是至关重要的。就吉布斯自由能本身而言，它作为生命体系赖以生存的能量，直接维持和驱动着生命体系的运转；就吉布斯自由能的变化而言，它可以作为生命过程能否自发进行的判据。4

本词条内容贡献者为:

李廉 - 副教授 - 中国矿业大学