导出分数就是指具有一定参考点和单位,且可以相互比较的分数量表或符号系统1。
定义导出分数就是在原始分数转换的基础上,按照一定的规则,经过统计处理后获得的具有一定参考点和单位,且可以相互比较的分数量表或符号系统。这种按某种规则将原始分数转化为导出分数的过程称为分数的转换。
常用的导出分数有百分等级分数、标准分数和T分数等1。
百分等级分数百分等级分数概念百分等级分数是应用最广的导出分数。一个原始分数的百分等级是指在一个群体的测验分数中,得分低于这个分数的人数的百分比。也就是说,如果将某一被试群体分为一个白个等级,则每位被试所占的等级数就是百分等级。例如,某一被试在一项测验中得分82分,经过换算,百分等级分数为75,就表示参加该项测验的人的得分低于82分的占全体被试的75%,并说明超过他的成绩82分的人仅有25%,我们通常PR用来表示百分等级。百分等级取值越大,说明成绩越优秀1。
百分等级分数计算百分等级的计算关键在于确定在常模团体中分数低于某一特别分数的人数比例,分两种情况:
1、未分组资料的百分等级计算,公式为:
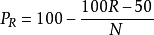
其中PR是原始分数排列顺序数,N是指总人数(样本的总人数)。例如小东在50名同学中语文成绩是80分,排列第9名,则其百分等级为:
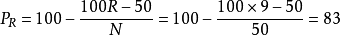
百分等级为83即指,在100名被试中,语文成绩低于小东的80分的有83人
2、分组资料的百分等级求法,虽然计算方法不同,但其百分等级的意义与未分组资料一样。
另一种是分组资料的百分等级计算,公式为:
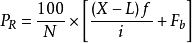
PR为百分等级;X为给定的原始分数;f为该分数所在组的频数;Fb为该分数所在组的精确下限;
Fb为X所在组以下各组次数的和;N为总次数;i为组距1。
百分等级的优缺点·优点
1:容易计算,容易解释,甚至外行人也能理解
2:对于各种被试和各种测验普遍适用
缺点
1:缺少相等单位属于顺序量表
2:测验分数的分布通常呈正态曲线,中间密集两端分散而百分等级的分布呈长方形,因此接近中数或分配中间的原始分数的差异在转换成百分等级时往往被夸大而接近分数两端的原始分数差异转换成百分等级后则被大大缩小1。
标准分数标准分数概念标准分数也叫z分数,是一种具有相等单位的量数。它是将原始分数与团体的平均数之差除以标准差所得的商数,是以标准差为单位度量原始分数离开其平均数的分数之上多少个标准差,或是在平均数之下多少个标准差。它是一个抽象值,不受原始测量单位的影响,并可接受进一步的统计处理1。
标准分数计算
用公式表示为:z=(x-μ)/σ
其中z为标准分数;x为某一具体分数,μ为平均数,σ为标准差。
标准分数的特点由z分数组成的分布有两个特点:一是z分数的平均等于0;二是其标准差等于1。当一组数据为正态分布或近似正态分布时,相当于平均数的点的标准分数为0,在平均数以上各点的标准分数为正值,在平均数以下的各点的标准分数为负值。
标准分数是一种不受原始测量单位影响的数值。其作用除了能够表明原数据在其分布中的位置外,还能对未来不能直接比较的各种不同单位的数据进行比较。如比较各个学生的成绩在班级成绩中的位置或比较某个学生在两种或多种测验中所得分数的优劣。
T分数T分数是一种标准分常模,平均数为50,标准差为10的分数。即这一词最早由麦柯尔于1939年提出,是为了纪念推孟和桑代克对智力测验,尤其是提出智商这一概念所作出的巨大贡献。
T分数的计算:T=10Z+50
T为T分数,Z为标准分数1。
标准九分数标准九分是常态化标准分数的一种,主要是利用正态分布的概念,将正态分布的曲线分为九个部份。标准九分的平均值为 5,标准差为 2,单位为半个标准差,除了 1 分及 9 分之外,各分数的范围也是半个标准差1。
标准九分及正态分布的关系
|| ||
本词条内容贡献者为:
杨绍清 - 副教授 - 华北理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国