[科普中国]-理想气体分体积定律

理想气体分压定律描述的是理想气体的特性。这一经验定律是在1801年由约翰·道尔顿所观察得到的。同样的，理想气体分体积定律由理想气体分压定律推导而来，也是描述理想气体的特性。在任何容器内的气体混合物中，如果各组分之间不发生化学反应，则每一种气体都均匀地分布在整个容器内，它的体积分数和它对于整个系统的物质的量分数相同。

背景知识理想气体状态方程理想气体状态方程，又称理想气体定律、普适气体定律，是描述理想气体在处于平衡态时，压强、体积、物质的量、温度间关系的状态方程。它建立在玻义耳-马略特定律、查理定律、盖-吕萨克定律等经验定律上。

其方程为pV = nRT。这个方程有4个变量：p是指理想气体的压强，V为理想气体的体积，n表示气体物质的量，而T则表示理想气体的热力学温度；还有一个常量：R为理想气体常数。可以看出，此方程的变量很多。因此此方程以其变量多、适用范围广而著称，对常温常压下的空气也近似地适用。

满足理想气体状态方程且比热比为常数的气体，称为完全气体，从微观角度来看，它是分子本身体积与分子间作用力都可以忽略不计的气体。在常温常压下，实际气体分子的体积和分子间的相互作用也可忽略不计，状态参数基本能够满足理想气体状态方程，所以空气动力学常把实际气体简化为完全气体来处理。在低速空气动力学中，空气就可以被视为比热比为常数的完全气体；在高速空气动力学中，气流的温度较高，空气中气体分子的转动能和振动能随着温度的升高而相继受到激发，比热比不再是常数，在1500~2000K的温度范围内，空气可视为变比热比的完全气体。1

理想气体分压定律道尔顿分压定律（也称道尔顿定律）描述的是理想气体的特性。这一经验定律是在1801年由约翰·道尔顿所观察得到的。在任何容器内的气体混合物中，如果各组分之间不发生化学反应，则每一种气体都均匀地分布在整个容器内，它所产生的压强和它单独占有整个容器时所产生的压强相同。也就是说，一定量的气体在一定容积的容器中的压强仅与温度有关。例如，零摄氏度时，1mol 氧气在 22.4L 体积内的压强是 101.3kPa 。如果向容器内加入 1mol 氮气并保持容器体积不变，则氧气的压强还是 101.3kPa，但容器内的总压强增大一倍。可见， 1mol 氮气在这种状态下产生的压强也是 101.3kPa 。

道尔顿（Dalton）总结了这些实验事实，得出下列结论：某一气体在气体混合物中产生的分压等于在相同温度下它单独占有整个容器时所产生的压力；而气体混合物的总压强等于其中各气体分压之和，这就是气体分压定律（law of partial pressure）。

即理想气体混合物中某一组分B的分压等于该组分单独存在于混合气体的温度T及总体积V的条件下所具有的压力。而混合气体的总压即等于各组分单独存在于混合气体温度、体积条件下产生压力的总和。这即为道尔顿分压定律。

道尔顿定律只适用于理想气体混合物，实际气体并不严格遵从道尔顿分压定律，在高压情况下尤其如此。当压力很高时，分子所占的体积和分子之间的空隙具有可比性；同时，更短的分子间距离使得分子间作用力增强，从而会改变各组分的分压力。这两点在道尔顿定律中并没有体现。1

理想气体分压定律的推导首先，由理想气体状态方程推导出理想气体分压定律：

PV=nRT（1）

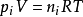（2）

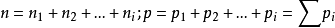所以，（3）

根据（1）和（2）可以得到，；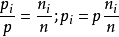

这就是理想气体分压定律。

而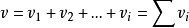

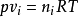
所以，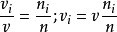

知识扩展实际气体状态方程

实际气体都不同程度地偏离理想气体定律。偏离大小取决于压力、温度与气体的性质，特别是取决于气体液化的难易程度。对于处在室温及1大气压左右的气体，这种偏离是很小的，最多不过百分之几。如氧气和氢气是沸点很低的气体（-183摄氏度和-253摄氏度），在25摄氏度和1大气压时，摩尔体积与理想值的偏差在0.1%以内。而沸点较高的二氧化硫和氯气(-10摄氏度与-35摄氏度)，在25摄氏度与1大气压下就不很理想。它们的摩尔体积比按理想气体定律预计的数值分别低了24%与16%。当温度较低、压力较高时，各种气体的行为都将不同程度地偏离理想气体的行为。此时需要考虑分子间的引力和分子本身的体积重新构造气体状态方程。1

本词条内容贡献者为:

李廉 - 副教授 - 中国矿业大学