定律定义二维的情形
(1)平面上的单连通区域与复连通区域
设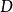 是平面
是平面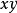 上的区域。如果
上的区域。如果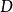 内的任何封闭曲线
内的任何封闭曲线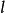 所围成的区域
所围成的区域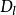 ,恒有
,恒有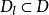 ,则
,则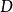 称为单连通区域;否则,
称为单连通区域;否则,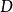 称为复连通区域。
称为复连通区域。
(2)平面曲线积分与路径无关的条件
定理11 设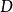 是平面
是平面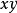 上的单连通闭区域,函数
上的单连通闭区域,函数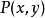 与
与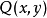 在
在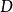 内具有一阶连续偏导数,则下列
内具有一阶连续偏导数,则下列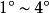 两两等价
两两等价
 沿
沿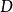 内任何光滑闭曲线
内任何光滑闭曲线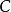 ,恒有
,恒有
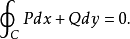
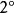 对
对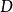 内的曲线积分
内的曲线积分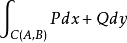 ,只与这光滑曲线
,只与这光滑曲线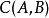 的起点
的起点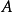 、终点
、终点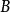 有关,而与路径无关,即恒有
有关,而与路径无关,即恒有
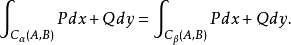
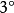
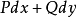 在
在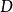 内是某一个函数
内是某一个函数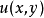 的全微分,即在
的全微分,即在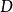 恒有
恒有
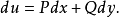
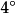 在
在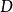 内每一点处恒有
内每一点处恒有
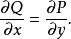
三维的情形(1)曲面单连通区域与曲面复连通区域
设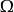 是
是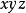 空间的区域。如果
空间的区域。如果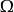 内的任何简单封闭曲线
内的任何简单封闭曲线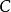 ,都存在以
,都存在以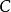 为边界的曲面
为边界的曲面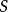 ,使得
,使得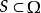 ,则
,则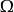 称为曲面单连通区域;否则,
称为曲面单连通区域;否则,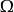 称为曲面曲面复连通区域。
称为曲面曲面复连通区域。
(2)空间曲线积分与路径无关的条件
定理21 设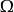 是平面
是平面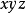 空间的曲面单连通闭区域,函数
空间的曲面单连通闭区域,函数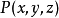 、
、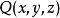 、
、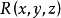 在
在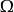 内都具有一阶连续偏导数,则下列
内都具有一阶连续偏导数,则下列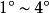 两两等价
两两等价
 沿
沿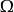 内任何光滑闭曲线
内任何光滑闭曲线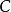 ,恒有
,恒有
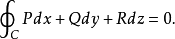
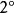 对
对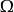 内任何一个光滑曲线段
内任何一个光滑曲线段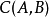 ,曲线积分
,曲线积分
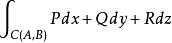
仅与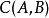 的起点
的起点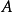 、终点
、终点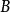 有关,而与路径无关。
有关,而与路径无关。
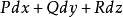 在
在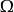 内是某一个函数
内是某一个函数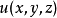 的全微分,即在内恒有
的全微分,即在内恒有
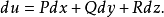
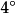 在
在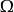 内每一点处恒有
内每一点处恒有

应用领域上述两类定理条件中要求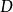 和
和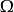 为单连通区域是很重要的。如下面的例子:
为单连通区域是很重要的。如下面的例子:
例 12 计算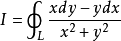 ,其中
,其中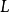 为任一不包含原点的闭区域
为任一不包含原点的闭区域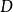 的边界曲线,分段光滑.
的边界曲线,分段光滑.
解 因为
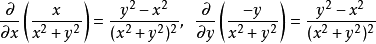
在区域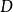 上连续且相等,于是
上连续且相等,于是
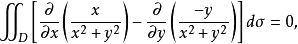
所以根据格林公式即可得
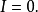
倘若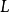 为绕原点一周的封闭曲线,则函数
为绕原点一周的封闭曲线,则函数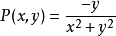 ,
,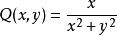 只在剔除原点外的任何区域
只在剔除原点外的任何区域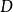 上有定义,所以
上有定义,所以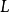 必含在某个复连通区域内。这时它不满足定理1的条件,因而就不能保证
必含在某个复连通区域内。这时它不满足定理1的条件,因而就不能保证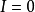 成立。事实上,设
成立。事实上,设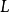 为绕原点一周的圆
为绕原点一周的圆
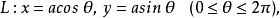 则有
则有
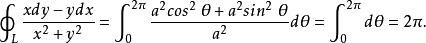
若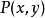 ,
,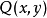 满足定理1的条件,则由上述证明可看到二元函数
满足定理1的条件,则由上述证明可看到二元函数
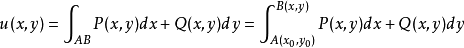 具有性质
具有性质
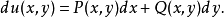 它与一元函数的原函数相仿。所以我们也称
它与一元函数的原函数相仿。所以我们也称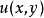 为
为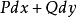 的一个原函数。
的一个原函数。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国