概念
1932年,Wigner在量子力学中引进了时间反演,乍一看来,这是与空间反演相似的一个分立对称性,实际上不然。这是用词不当。严格地说,所谓的时间反演对称乃是指运动的可逆性,即把一个过程用摄像机拍下来,然后把胶卷倒过来放映,假如看上去运动规律(当然不是指“现象”)与顺放时一样,就叫做“时间反演守恒”。1
基本原理对一个无自旋粒子在位形空间写出薛定谔方程:
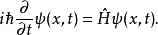
按上述定义,让我们先作变换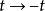 ,看变换后对
,看变换后对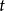 的薛定谔方程是否能保持与原来有同样形式?显然不能!这时因为方程对
的薛定谔方程是否能保持与原来有同样形式?显然不能!这时因为方程对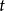 的微商是一阶而非二阶的缘故。于是在第二步,对整个方程取一次复共轭运算,才能得到预期的“时间反演不变的”薛定谔方程。
的微商是一阶而非二阶的缘故。于是在第二步,对整个方程取一次复共轭运算,才能得到预期的“时间反演不变的”薛定谔方程。
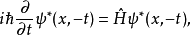 其中已假设
其中已假设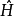 不含时间,于是原来的
不含时间,于是原来的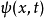 与
与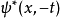 这两个解之间有某种对称性或等价性的关系。这是可能的,试看一个定态波函数,我们有:
这两个解之间有某种对称性或等价性的关系。这是可能的,试看一个定态波函数,我们有:
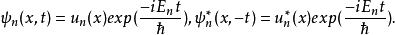 于是有两种可能性:
于是有两种可能性:
(1)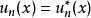 是实函数,
是实函数,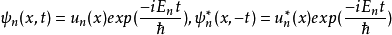 的两个态是同一个态。即当
的两个态是同一个态。即当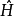 在时间反演下不变且本征态
在时间反演下不变且本征态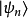 (在能量上)非简并时,其相应之本征波函数必可写成(实函数)
(在能量上)非简并时,其相应之本征波函数必可写成(实函数)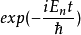 的形式。
的形式。
(2)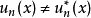 ,
,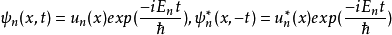 的两个态不同,但有同样的能量
的两个态不同,但有同样的能量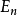 ,所以是简并态。例如在中心势场中的能量本征态
,所以是简并态。例如在中心势场中的能量本征态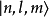 ,
,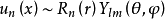 ,而
,而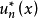 对应于
对应于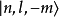 ,当
,当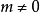 时,它们是简并的,且互为“时间反演态”。另一粒子是平面波,此时
时,它们是简并的,且互为“时间反演态”。另一粒子是平面波,此时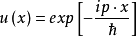 ,它与
,它与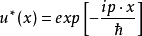 在能量上简并。2
在能量上简并。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国