MIS结构指金属-绝缘层-半导体结构 ,是研究半导体表面效应的重要方面。许多半导体器件的特性都和半导体的表面性质有着密切的关系。例如,半导体的表面状态和半导体集成电路的参数和稳定性有很大影响。在某些情况下,往往不是半导体的体内效应,而是其表面效应支配着半导体器件的特性。例如MOS(金属—氧化物—半导体)器电,就是利用半导体表面效应而制成的。因此,研究半导体表面究象,发展有关半导体表面的理论,对MIS结构的研究,对于改善器件性能,提高器件稳定性,以及指导人们探索新发器件等都有着十分重要的意义。1
简介一个金属-绝缘层-半导体(MIIS)结构是一片绝缘层被夹在金属层和半导体层之间。并且,一个MIS结构的直流电导为零。半导体通常在背后有一个欧姆接触。绝缘体通常选择使用其半导体的氧化物。特别的,把二氧化硅做在硅表面上的工艺是非常先进成熟的,由这种氧化物工艺形成的结构,叫做MOS(Metal-oxide-Semiconductor)结构。而且这种结构极其重要,可以用来研究半导体表面、整合电子电路或者和用于CMOS(Complementary Metal Oxide Semiconductor/互补金属氧化物半导体)技术,而且CCDs(charge-coupled devices/电荷耦合器件)也是基于这种MIS结构2
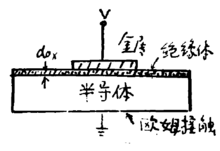
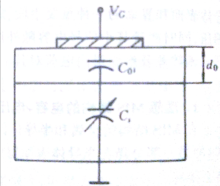
理想的MIS结构/空间电荷层及表面势金属一绝缘体一半导体结构(简称MIS结构),如图所示。以氧化物(例如硅的氧化物Sioz)作为绝缘体,就叫MOS结构。MOS是构成晶体管的基本结构。在金属端加正电压(称为控制极电压)时,取作V>O。
图中表示V=O时,n型/p型半导体的理想MIS结构的能带。这里Ei是本征半导体的费米能级,e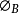 是费米能级Es和Ei的差。
是费米能级Es和Ei的差。
理想MIS结构的定义如下:
(i)v=o时,半导体的能带是平坦的(称为平面能带),换言之,v=o时,金属和半导体的功函数相等。如右图所示,这个条件可写成下式:3
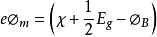 (ii)v
(ii)v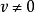 时,对于p型半导体
时,对于p型半导体
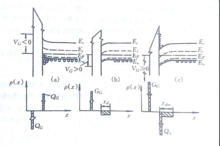
(1)多数载流子堆积状态
当金属与半导体间加负电压(指金属接负)时,表面势为负值,表面处能带向上弯曲,。在热平衡情况下,半导体内费米能级应保持定值,故随着向表面接近,价带顶将逐渐移近甚至高过费米能级,同时价带中空穴浓度也将随之增加。这样,表面层内就出现空穴的堆积而带正电荷。从图中还可看到,越接近表面空穴浓度越高,这表明堆积的空穴分布在最靠近表面的薄层内。
(2)多数载流子耗尽状态
当金属与半导体间加正电压(指金属接正)时,表面势Vs为正值,表面处能带向下弯曲。这时越接近表面,费米能级离价带顶越远,价带中空穴浓度随之降低。在靠近表面的一定区域内,价带顶位置比费米能级低得多,根据玻耳兹曼分布,表面处空穴浓度将较体内空穴浓度低得多,表面层的负电荷基本上等于电离受主杂质浓度。表面层的这种状态称做耗尽。
(3)少数载流子反型状态
当加于金属和半导体间的正电压进一步增大时,表面处能带相对于体内将进一步向下弯曲。这时,,表面处费米能级位置可能高于禁带中央能量Ei,也就是说,费米能级离导带底比离价带顶更近一些。这意味着表面处电子浓度将超过空穴浓度,即形成与原来半导体衬底导电类型相反的一层,叫做反型层。反型层发生在近表面处,从反型层到半导体内部还夹着一层耗尽层。在这种情况下,半导体空间电荷层内的负电荷由两部分组成,一部分是耗尽层中已电离的受主负电荷;另一部分是反型层中的电子,后者主要堆积在近表面区。
对于n型半导体,不难证明,当金属与半导体间加正电压时,表面层内形成多数载流子电子的堆积:当金属与半导体间加不太高的负电压时,半导体表面内形成耗尽层;当负电压进一步增大时,表面层内形成有少数载流子空穴堆积的反型层。
表面空间电荷层的电场、电势和电容为了深入分析表面空间电荷层的性质,可以通过解泊松方程定量的求出表面层中电场强度和电势分布,
取x轴垂直于表面指向半导体内部,并现定表面处为x轴原点。在表面空间电荷层中的电荷密度、场强和电势都是x的函数,把表面近似看成是无限大面,以上各量将不随y,z变,所以看成一维情况来处理。在这种情况下,空间电荷层电势满足的泊松方程为:
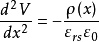
式中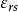 为半导体的相对介电常数,
为半导体的相对介电常数,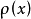 为总的空间电荷密度,且由下式给出
为总的空间电荷密度,且由下式给出
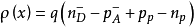
其中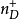 ,
,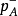 分别表示电离施主和电离受主浓度,
分别表示电离施主和电离受主浓度,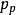 和
和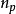 分别表示坐标x点的空穴浓度和电子浓度。若考虑表面层中经典统计 仍能使用的情况,则在电势V的x点(取半导体内部电势为零),电子和空穴浓度分别为
分别表示坐标x点的空穴浓度和电子浓度。若考虑表面层中经典统计 仍能使用的情况,则在电势V的x点(取半导体内部电势为零),电子和空穴浓度分别为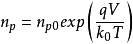
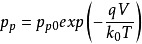
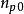 和
和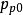 分别表示半导体体内的平衡电子和空穴浓度。在半导体内部,假定表面空间电荷中电离杂质浓度为一常数,且与体内相等,则在半导体内部,电中性条件成立,故有
分别表示半导体体内的平衡电子和空穴浓度。在半导体内部,假定表面空间电荷中电离杂质浓度为一常数,且与体内相等,则在半导体内部,电中性条件成立,故有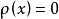 ,即
,即
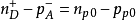
将上述三式带入泊松方程得
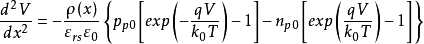
将上式两边乘以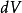 Bn并积分,并考虑
Bn并积分,并考虑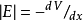 ,得
,得
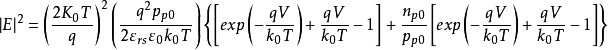
令
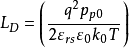
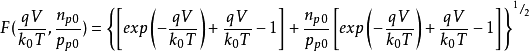
则
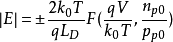
当V大于零时取“+”号,小于零时取“-”号,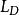 称为德拜长度。F函数是表征半导体空间电荷层的一个重要参数。通过F函数,可以方便地表面空间电荷层的基本参数表达出来。
称为德拜长度。F函数是表征半导体空间电荷层的一个重要参数。通过F函数,可以方便地表面空间电荷层的基本参数表达出来。
在表面处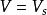 ,可得到半导体表面处的电场强度为
,可得到半导体表面处的电场强度为
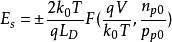
根据高斯定理,表面的电荷密度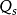 与表面处电场强度有以下关系:
与表面处电场强度有以下关系:
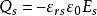
将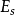 代入上式,则
代入上式,则
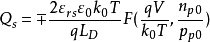
当金属电极为正,即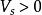 时,
时,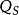 用负号;反之,
用负号;反之,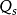 用正号。从式中还能看到,表面层存在电场时,载流子浓度也发生变化。在单位面积的表面层中空穴的改变量(与体内比较)为
用正号。从式中还能看到,表面层存在电场时,载流子浓度也发生变化。在单位面积的表面层中空穴的改变量(与体内比较)为
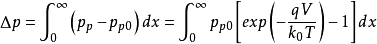
考虑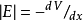 ,并且
,并且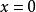 ,
,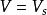 和
和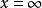 ,
,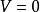 ,则
,则
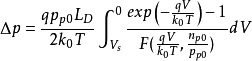
同理可得
以上两式在计算电导时常要用到。根据 式子,
式子, 随
随 而变,这相当于一电容效应。微分电容可由
而变,这相当于一电容效应。微分电容可由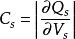 求得为
求得为
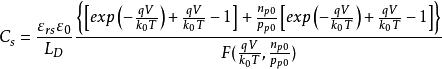
上式给出的单位面积上的电容,单位为国际单位。于是应用上面得到的公式可定量的分析各种表面层的状态
多数载流子堆积状态仍以p型半导体来说明。当外加电压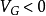 时,表面势及表面层内部的电势V都是负值,对于足够大的
时,表面势及表面层内部的电势V都是负值,对于足够大的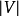 和
和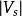 值。F函数只有含
值。F函数只有含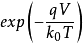 的项其主要作用,其他项都可略去,得
的项其主要作用,其他项都可略去,得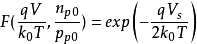
将上面公式带入之前公式,得
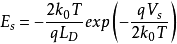
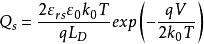
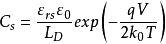
上述三式分别表示出在多数载流子堆积状态时,表面电场、表面电荷和空间电荷电容随表面势变化的关系
平带状态外加电压为零时,表面势等于零,表面处能带不发生弯曲,称作平带状态。这时很容易求得F函数为零,从而Es=0,Qs=0。表面空间电荷层电容不能直接以Vs=0 得到,因为给出的时不稳定值。所以对原式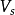 展开,近似取到二次方项,并令
展开,近似取到二次方项,并令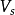 趋近于零,并考虑到
趋近于零,并考虑到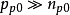 ,最终得到
,最终得到
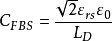
耗尽状态当外加电压为正但其大小还不足以使表面处禁带中央能量弯曲到费米能级以下时,表面不会出现反型,空间电荷区处在空穴耗尽状态,这时V和Vs都大于零,且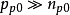 ,经过省略,则
,经过省略,则
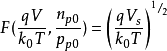
又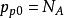 带入,得
带入,得
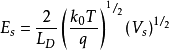
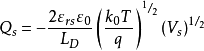
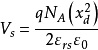
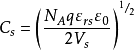
也可以由“耗尽曾近似”直接处理,直接写出电荷密度,泊松方程
反型状态随着外加正电压增大,表面出禁带中央能值可以下降到费米能级以下,出现反型层。反型状态分为强反型和弱反型两种,以表面处少数载流子浓度是否超过体内多数载流子浓度为标志来定。根据载流子浓度公式和玻尔兹曼统计可推得发生强反型的条件为:Vs≥2VB
在临界强反型时
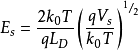
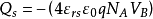
当Vs 比2VB 大很多时,而且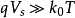 时,有
时,有
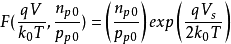
将上式带入原公式,得
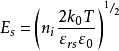
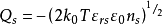
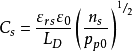
MIS结构电容电压特性理想MIS结构的电容-电压特性考虑理想情况,由理论推导可得到
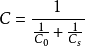
表明MIS结构电容相当于绝缘层电容和半导体空间电荷层电容串联,下面讨论理想MIS结构的电容电压特性。
当偏压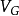 为负值时半导体表面处于堆积状态,将此时的空间
为负值时半导体表面处于堆积状态,将此时的空间
电荷层的电容公式带入上式中,得到
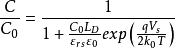
可以看出当加较大的负偏压时C=C0,此时的MIS的电容不随外加电压的变化。当|VG|较小时,|Vs|也很小,上式分母第二项变大,此时C/C0随|Vs| 的减小而减小,如图中BC段所示。
当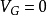 时,同理将之前所求电容公式代入,得
时,同理将之前所求电容公式代入,得
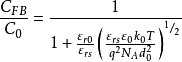
在利用C-V特性测量表面参数时常需计算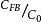 的值因此根据上式做了一簇曲线以供查
的值因此根据上式做了一簇曲线以供查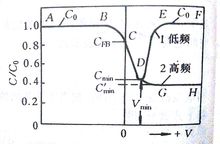 阅。在图中可以看到若绝缘层厚度一定,NA越大CFB/C0 也越大,这是因为表面空间电荷层随
阅。在图中可以看到若绝缘层厚度一定,NA越大CFB/C0 也越大,这是因为表面空间电荷层随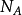 增大而变薄所致。另一方面绝缘层厚度越大,C0越小,CFB/C0 也越大。
增大而变薄所致。另一方面绝缘层厚度越大,C0越小,CFB/C0 也越大。
当金属与半导体间外加偏压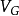 为正但不足以使半导体表面反型时,空间电荷区处于耗尽状态,同理将此时的电容公式带入,得
为正但不足以使半导体表面反型时,空间电荷区处于耗尽状态,同理将此时的电容公式带入,得
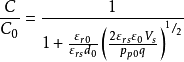
上式表明,MIS结构电容随表面势变化情况。因VG=V0+VS, V0=-Qs/c0,,又由之前得到的Qs公式,求解Vs,化简整理后得
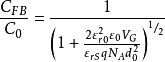
上式表示在耗尽状态时C/C0 随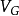 变化情况。从上式可以看出,当
变化情况。从上式可以看出,当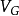 增加时,C/C0 将减小。如图中CD段表示当外加电压增大到
增加时,C/C0 将减小。如图中CD段表示当外加电压增大到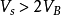 时,此时耗尽层宽度保持在极大值,表面处出现反型层,同理得到
时,此时耗尽层宽度保持在极大值,表面处出现反型层,同理得到
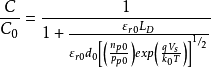
上式表示在强反型情况下时C/C0 随表面势的变化情况。可以看出上式分母中第二项趋近于零,这时C=C0 ,即MIS的电容又上升到等于绝缘层的电容,如图中EF段表示。
当信号变为高频时上式不再适用,图像如GH段所示1
金属与半导体功函数差对C-V特性的影响为了具体起见,以铝-二氧化硅-硅组成的MOS结构为例来说明,并设半导体硅为P型的。将铝和p型硅连接起来,由于p型硅的功函数一般较铝为大,电子将从金属流向半导体中。因此在p型硅表面层内形成带负电的空间电荷层,而在金属表面产生正电荷。这些正负电荷在二氧化硅及硅表面层内产生指向半导体内部的电场,并使硅表面层内能带发生向下弯曲。同时硅内部的费米能级相对于金属的费米能级就要向上提高,到两者相等达到平衡,所以半导体中电子的电势能相对于金属提高的数值为
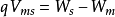 由于二者功函数不同,即使外加偏压为零,但半导体表面层并不处于平带状态,所以为了恢复这一状态,必须在铝和半导体硅之间加一个负电压,这个负电压就是
由于二者功函数不同,即使外加偏压为零,但半导体表面层并不处于平带状态,所以为了恢复这一状态,必须在铝和半导体硅之间加一个负电压,这个负电压就是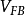 。显然:
。显然:
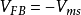
绝缘层中电荷对C-V特性的影响
一般在MIS结构的绝缘层内总是或多或少地存在着电荷的,设绝缘层中有一薄层电荷,其单位面积上的电量为
Q,离金属表面的距离为x在无外加电压时,这薄层电荷将分别在金属表面和半导体表面层中感应出相反符号的电荷。由于这些电荷的存在,在半导体空间电荷层内将有电场产生,能带发生弯曲。这就是说,虽然未加外电
压,但由于绝缘层内电荷的作用,也可使半导体表面层离开平带状态。为了恢复平带状态,同前一样,必须在金属板上加一定的偏压。例如,Q是正电荷时,在金展与半导体表面层中将感应出负电荷空间电荷层发生能带向下弯曲。若在金属板上加一逐渐增大的负电压,金属板上的负电荷将随之增加,由Q发出的电力线特更多地终止于金属表面。半导体表面层内的负电荷就会不断减小,如果外加负电压增大到这样程度,以致使半身体表面层内的负电荷完全消失了。这时,在半导体表面层内。由薄层电荷所产生的电场完全被金属表面负电荷产生的电场所抵消,表面层能带的弯曲也就完全用失。
这时,经计算
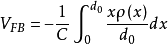
当上述二者都存在时
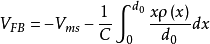
本词条内容贡献者为:
陈红 - 副教授 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国