直道线是关于C-曲面的一个概念,是指C-曲面的直径面截口。极限球面的“直道线”是指它的直径面截口,即属于已知极限球面的极限圆。球面的直径面截口,即它的大圆叫作直道线。
C-曲面线把的C-曲面为点的轨迹,这些点都在线把内的半线上,且和线把内某一条选定的半线上某一个起点对应,线把内的半线都叫作这个C-曲面的轴。三种类型的线把分别为:聚集线把,分散线把和平行线把。
聚集线把的C-曲面为与线把的中心有等距离的点的轨迹,这就是球面,它也可以看成一个圆周绕着它的直径旋转所成的曲面。
事实上,因为曲面上任意两个对应点所在的半线相交于线把的中心,那么,它们和线把的中心等距离,曲面的直径面截口上各点也和线把的中心等距离,故截口为一个圆,把这个圆绕直径旋转便得已知球面。
分散线把的C-曲面为与一平面等距离的点的轨迹,它和线把的底面重合,这曲面叫作等距曲面或叫作超球面。超球面为超圆绕着它的轴旋转所成的曲面。
事实上,因为曲面上任意两个对应点分别在分散线把的两条半线上,那么,它们和线把的底面等距离。依同理,曲面的一切直径面截口为超圆,且互相全等,一个超圆绕着它的轴旋转便得超球面。
平行线把的C-曲面叫作浑球面或叫作极限球面,它是极限圆绕着它的轴旋转所成的曲面。
事实上,极限球面的直径面截口上的一切点,在直径面上一个平行半线束里的半线上互相对应,故为一个极限圆。这极限圆绕着它的轴旋转便得极限球面。
极限球面的直道线极限球面定义极限球面是罗巴切夫斯基空间中的一种曲面,它是由极限圆绕其一个轴旋转而生成的。空间中的极限球面相当于平面上的极限圆,因此,极限球面亦可以定义为一种轨迹,过直线a上某点M在一定方向上向空间中所有与该直线平行直线引斜率相等的截线,截线端点的轨迹就是一极限球面,点M叫做极限球面之球心, 直线a叫做极限球面的轴。若已知轴a及轴上一点M,则极限球面便已确定。
极限球面又叫极曲面。
定理1线把的C-曲面为点的轨迹,这些点都在线把内的半线上,且和线把内某一条选定的半线上某一个起点对应,线把内的半线都叫作这个C-曲面的轴。
定理3平行线把的C-曲面叫作浑球面或叫作极限球面,它是极限圆绕着它的轴旋转所成的曲面。
事实上,极限球面的直径面截口上的一切点,在直径面上一个平行半线束里的半线上互相对应,故为一个极限圆。这极限圆绕着它的轴旋转便得极限球面。
定理4一切极限球面全等。
定理5经过极限球面上一点的平面,或者和它相切,或者和它相交于一圆或一极限圆。
极限球面上的直道线极限球面上的绝对几何学
我们的目的是要建立极限球面上的内在几何学,这在叙述罗巴切夫斯基几何学进一步的发展时,是有极重要的意义的,我们在这里要努力使建立这种几何学的程序,尽可能地和建立平面几何学的程序接近,正如在平面几何学一样,我们首先建立基本概念和起公理作用的基本命题,然后对由这些命题所得到的推论做一概述,但我们现在既然已经知道了极限球面在空间的性质,那么,和平面几何学不同,极限球面上的几何学的基本概念,将不是没有定义的名词,而将给以定义,同样,它的基本命题也不是公理,而是罗巴切夫斯基空间几何学的定理。
类似地,我们引进极限球面上的几何学的基本概念。
1) 所谓“点”是指已知极限球面上的点。
2) 所谓极限球面的“直道线”是指它的直径面截口,即属于已知极限球面的极限圆。
3) 如果点在极限圆上,我们说点和直道线相关联。
4) 如果在平面ABC上,极限球面的轴BB’介于两轴AA'和CC’之间,我们说:在直道线ABC上,点B介于点A和点C之间。
5)所谓图形的“运动”是仅指那些运动,当运动时,图形的各点经常保留在已知的极限球面上1。
相关性质我们现在来列举一些命题,在这里即需指出,这些命题和平面几何学的公理是相类似的。
1. 经过极限球面上两个不相同的点,在这曲面上有一条且仅有一条直道线。 经过极限球面的任意两点A,B有一个且仅有一个直径面,而极限球面上的极限圆就是它和直径面的交线。
2. 在每条直道线上最少有两点。
3. 有不在同一直道线上的三点存在。
4. 同一直道线上三个不同的点之中,总有且仅有一点介于其他两点之间。
5. 设A,B为两个不同的点.则在直道线AB上,存在着无穷多点介于A和B之间,也存在着无穷多点,使点B介于点A和它们中任何一点之间。
6. 直道线上任何点O,划分它上面其余的点为两类,使点O介于任何不同类的两点之间,但不介于同类的两点之间。
7. 极限球面上的直道线把它划分为两个凸区域。
8. 极限球面上两个运动继续举行的结果,也是极限球面上的运动;又极限球面上每个运动的逆运动,也是极限球面上的运动。
9. 极限球面上的运动,把直道线段变为直道线段。这是很明显的,因为经过运动之后,极限圆仍是极限圆,在它弧上的点仍留在弧上。
10. 在极限球面上,正如在其他每个C-曲面上一样,极限球面在其自身上有移转的自由。
11. 存在着这样的运动,把直道线段AB变为直道线段BA。又把这两个直道线段的夹角AOB,变为角BOA。
12. 如果把极限球面上有向直道线上各点,划分为两个戴德金特的类,那么,或者在第一类里有最后的点,或者在第二类里有最前的点。
极限球面上的弧和角应用以上所述的这些命题,我们可以建立相等的概念,那是对于极限圆的弧段和在极限球面上同过一点的两弧所成的夹角来说的,如果两个弧段或两个角经过运动后彼此叠合,我们便说两弧相等,或两角相等。通常的办法,我们建立补角和对顶角的概念,并把极限球面上的圆定义为自极限球面上一点出发的等长极限圆弧的终点的轨迹,我们容易见到这样定义的“极限球面上的圆”,对于外围空间来说,也是一个圆。事实上,设在极限球面上,给定一段极限圆弧OM,那么,把这弧在极限球面上绕着点O而转动,它画成一个圆,这是依照极限球面的内在几何学的意义来说的,但点M的运动,同时也是它绕着极限球轴OO'的转动,由于这样的运动,它显然也画出一个圆。这是依照外围空间的几何意义来说的。
由平面几何学中关于相等的角和全等三角形的定理,我们可以得到关于极限圆弧所作成的角和三角形的相等关系的定理。
取不相等的极限圆弧,或极限圆弧所夹的不相等的角,把一个放在另一个之上,我们也像在平面几何学里比较不相等的线段和角一样,可以确定它们孰大孰小,因以得到关于不等式的定理,这和平面几何学里对应的定理完全类似。特别的例子有,如极限圆弧所作成的三角形,我们得到它的每边小于其他两边之和的定理,由此定理又可推得:极限球面的直道线同时也是极限球面上联结两点的所有曲线中最短的曲线。
最后,与平面几何学里所建立的关于线段和角的测度理论完全相仿,我们建立极限圆弧和这些弧所夹的角的测度理论。
定理6如果每一极限圆弧段取得正数,令:1)相等的弧段取同一个数;2) 弧段的和所取的数,等于被加弧段所取的数之和,那么,对于所有的弧段,这个数等于用某个弧段单位去测量它们所得的长度。
定理7如果每一为两个极限圆弧所夹的角,取得正数,令:1)相等角取得同一个数,2)两角之和所取的数,等于被加角所取的数之和,那么,任何角所取的数,等于用某个定角为单位去测量它所得的角量。
这两条定理可以用来比较在极限球面上内在几何学里测度的结果,和在外围空间的几何学里对于同一量的测度结果。
极限圆的弧长正如其他一切曲线的弧长一样,可以看作折线的周长的极限,其折线的每段都为直线而内接于该弧,用这方法,每段极限圆弧可用一个数表示,此数显然适合定理1的条件1) 和2),由此推得:
如果把极限圆的弧长定义为它的内接折线的周长的极限,并令某段弧AB的长等于1,那么,在极限球面的内在几何学里任意另一段的弧长,等于以弧AB 为长的单位来测量该弧所得的结果。
同样地,在外围空间两条曲线所成之角,便是它们在交点的切线所成的夹角,把这个角的定义施用于相交的极限圆,我们对于每个这样的角,用一个数来代表,这个数适合定理2的条件1) 和2),由此推得:
如果把两个相交极限圆弧OA,OB 的切线的夹角取为角的单位,那么,在极限球面的内在几何学里,用两弧OA,OB 的夹角AOB 为单位,来量任何其他两个极限圆弧的夹角所得的结果,和它们的切线的夹角相同。换句话说,在极限球面的内在几何学里,两个极限圆的夹角,便是在它们交点和极限圆相切的两条直线所夹的角。
极限球面上的平行理论13. 经过极限球面上不属于直道线CD的点A,只能作一条直道线AP,直道线CD不相交。
和平行公理比较,我们可见在极限球面的内在几何学里,这条基本命题,可从欧几里得几何学的平行公理得来,如果把这公理的“直线”这个名词改为“直道线”,把“平面”改为“极限球面”的话。
现在检阅极限球面的内在几何学中所有13条基本命题,它们都可由欧几里得平面几何学公理得来,只需把“直线”这个名词改为“直道线”,把“平面”改为“极限球面”便成,因此,欧几里得平面几何学中所有的定理,在极限球面的内在几何学中依然成立,只需把其中的“直线”改为“直道线”,把其中的“平面”改 为“ 极限球面”。
换句话说,极限球面的内在几何学和欧几里得平面几何学的差别,只在两个基本概念有不同的名称。
这个著名的事实也是罗巴切夫斯基本人所发现的,并且对于非欧几里得几何学的建立,起了很重要的作用,这首先表示:如果根据任何理由,通使我们认为欧几里得公设对于平面几何学是不正确的,那么,这并非意味着欧几里得所建立的几何学失去了它的意义,它依然可以成立,不过不是在平面上,而是在极限球面上。
利用欧几里得公理系统现成的结果,我们得到一系列的事实,这些事实不但对于极限球面的研究是重要的,而且对于所有有关罗巴切夫斯基空间的研究,也同样重要。
从这些事实中我们提出下面几条:
1. 在极限球面上三个极限圆弧所围成的三角形,它的各内角之和等于两直角。
2.在极限球面上分别为极限圆弧所围成的两个三角形,称为彼此相似,如果它们的对应角相等,对应边成比例。
我们可以断定,在极限球面上,有彼此相似同时不相等的三角形存在,因为对于欧儿里得平面上的直线三角形,相对应的结果是成立的。
3.在极限球面上,组成三角形的极限圆的弧长与角间的关系,和在欧几里得平面上直线:三角形的边与角的关系相同。换句话说,欧几里得平面三角形中所有的关系式对于极限球面上的弧三角形都成立。
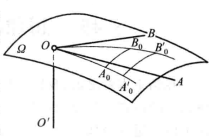
这个情形特别重要,因为它使我们可以给出在罗巴切夫斯基空间直线角的三角函数的几何定义。我们考虑半线OA,OB的夹角(图1),经过它的顶点O,作它的平面的垂线OO',经过点O,且以OO'为轴,作极限球面Ω,在这个极限球面上,作极限圆OA0和OB0分别和OA和OB相切,又过点B0作极限圆B0A0使弧OA0和A0B0所夹的角为直角,各弧OA0,A0B0,OB0的比值,和点B0的选择无关,因为在同一的顶角O,任意其他一个直角三角形OA'0B'0都和三角形OA0B0相似,然后,我们用通常方式,引入角AOB的三角函数的定义,得
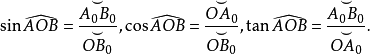
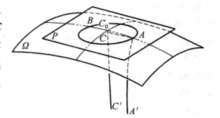
4.设在平面P 上给定一个圆,点C为圆心,CA 为半径(圆2),在点C作平面P的垂线CC'。过圆上点A作直线AA'和半线CC'平行,又在半线CC' 的延长线上求得点A 的对应点C0。在平面CC'A' 上,经过点C0,且以CC' 为轴的极限圆,应当经过圆周上的点A,因为点A 和点C0是对应点,再把这极限圆绕着轴CC'旋转,我们得到一个极限球面Ω,而所给的圆在这球面上,并且它在极限球面上的圆心为点C0,半径为极限圆弧C0A。
因此,每个圆都在某个极限球面上,且具有完全确定的极限圆弧半径。应用欧几里得几何学的相当定理,我们得到下面的结果:对于一切的圆,圆周的长度和它的极限圆弧直径的长度的比值是一个常数。我们熟知这个比值,用字母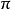 来表示的,是一个无理数,它约等于3.1416。
来表示的,是一个无理数,它约等于3.1416。
在罗巴切夫斯基几何学里所谓角的绝对量,是指以所给的角为圆心角时,圆弧的长度和这圆的极限圆弧半径的长度的比值。因为圆周的长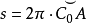 ,那么,角的绝对量
,那么,角的绝对量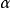 和它的角度
和它的角度 的关系,可表以通常公式
的关系,可表以通常公式
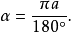
超球面上的直道线关于在罗巴切夫斯基空间超球面上和球面上的内在几何学的问题,仿照极限球面上讨论过的情形,我们可以把超球****面上的直道线当作它的直径面的截口,这些曲线显然是等距曲线,它们的底线在超球面的底面上.我们不难证明:如果把“极限球面”这个名词改为“超球面”,上面所有极限球面的相关性质1~12依然成立。因此,如果我们把“直线”改为“直道线”,把“平面”改为“超球面”,那么,绝对平面几何学的所有的定理依然成立。特别是这里仍可仿照极限球面上的同样办法,用两条切线所夹的角去量两条直道线或超圆弧所夹的角。
利用上面最后所说的,我们可以简单地解决超球面几何学中关于平行公理的问题,为此目的,我们考虑超球面上的三角形ABC,把这个弧三角形ABC投射到超球面的底面上,得直线三角形A'B’C'(图3**)**,这两个三角形的对应角两两相等,因为它们是同一个二面角的直线角,但三角形A'B'C'为罗巴切夫斯基平面上的直线三角形,故它的内角之和小于两直角。因此,超球面上由直道线即超圆弧所组成的三角形ABC,其内角的和也小于两直角。
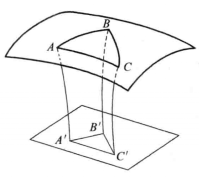
但我们知道,关于三角形内角和的命题,与平行公理等价。因此,在超球面上的几何学中,平行理论的基本命题可由罗巴切夫斯基平面几何学的平行公理推得。由此推知,如果在罗巴切夫斯基平面几何学里,把“直线”这个名词改为“直道线”,把“平面”改为“超球面”。那么,其中所有的定理仍然成立1。
球面上的直道线至于球面上的内在几何学问题,便与上述两款完全不同,设把球面的直径面截口,即它的大圆叫作直道线,我们将见,第1条公理便不可能成立。因为根据这公理,直线被它的两点所决定,但经过球径的两个端点,可作无穷多个大圆,而不是唯一的一个。关于点的顺序的基本命题也不成立,因为大圆是封闭曲线,若在其上取三点(图4),那么,究竟哪一点应该看作介于其他两点之间是一个不能唯一地解决的问题。
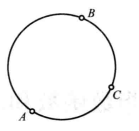
因此,就一般来说,绝对几何学的定理,在把“直线”和“平面”改为“大圆”和“球面”之后便不再成立。
其次,在球面的内在几何学,下面命题成立:“球面上每两条直道线必相交”,而在欧几里得几何学或在罗巴切夫斯基几何学,都没有和此相类似的命题。最后,我们还要注意,球面三角形内角之和大于两直角,这可由绝对空间几何学中熟知的定理直接推得,因为在三面角中,三个二面角之和大于两直角。
因此球面几何学与欧几里得几何学,正如它和罗巴切夫斯基几何学一样,有深刻的区别,我们也可用公理的方法来叙述球面几何学,黎曼曾经建立一支几何学,和球面几何学较相接近,他还把那种几何学的空间加以推广。在文献上,有时称那支几何学为黎曼几何学,或椭圆式几何学。与此相仿,罗巴切夫斯基几何学也称为双曲式几何学,欧几里得几何学也称为抛物式几何学1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国