立方倍积问题(problem of duplication of a cube)亦称倍立方体问题、德里安问题、Delos问题、德洛斯问题 、第罗斯问题等,是几何三大问题之一。假设已知立方体的棱长为a,所求立方体的棱长为x,则x3=2a3,令a=1,有x3-2=0。可以证明,若此方程有有理根,不外乎±1,±2,但它们都不是方程的根,因而不存在有理根,根据“有理系数的三次方程若无有理根,则长度等于它的任何实根的线段不能仅用尺规作图”的定理,立方倍积属尺规作图不能问题1。
基本介绍立方倍积就是利用尺规作图作一个立方体,使其体积等于已知立方体的二倍,这个问题也叫倍立方问题,也称之为德里安问题、Delos问题。
若已知立方体的棱长为1, 则立方倍积问题就可以转化为方程 解的尺规作图问题。根据尺规作图准则,该方程之解无法作出,因此,立方倍积问题和三等分角问题、化圆为方问题一起,成为古希腊三大几何难题。立方倍积问题不能用尺规作图方法解决的严格证明是法国数学家万采尔(P.-L. Wantzel,1814-1848)于1837年给出的2。
解的尺规作图问题。根据尺规作图准则,该方程之解无法作出,因此,立方倍积问题和三等分角问题、化圆为方问题一起,成为古希腊三大几何难题。立方倍积问题不能用尺规作图方法解决的严格证明是法国数学家万采尔(P.-L. Wantzel,1814-1848)于1837年给出的2。
立方倍积问题也叫第罗斯问题,传说爱琴海中第罗斯(Delos)岛上发生瘟疫,人们求教于巫神,祈求去病除邪妙方,巫神说神谕:要去病除邪,须把神殿前立方体祭坛的体积扩大一倍,第罗斯人把原祭坛棱长放大一倍,发现新祭坛体积不是原祭坛之二倍,这时瘟疫流行更加严重,第罗斯人又去求教柏拉图(Plato,公元前428-前348),柏拉图告诉他们说巫神之意并不在于要双倍大的祭坛,而只是为借此谴责希腊人不重视数学,对几何不够尊崇。
立方倍积问题提出后,二千多年来许多数学家相继研究,发现只要不限于尺规作图,运用特殊曲线(如圆锥曲线、蚌线、蔓叶线等),或是运用其它作图工具,立方倍积问题是不难解决的。在这研究过程中,人们发现了不少特殊曲线,还发现了一些精确度很好的近似作图法,公元前4世纪门内玛斯(Menaechmus, 约前375-325)研究圆锥曲线时发现,利用圆锥曲线可以解决立方倍积问题,若要求线段x(方程 之根),可以作抛物线
之根),可以作抛物线 与
与 ,其交点横坐标即所求的
,其交点横坐标即所求的 。 也可以作抛物线
。 也可以作抛物线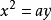 与双曲线
与双曲线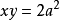 ,求交点的横坐标2。
,求交点的横坐标2。
立方倍积问题的解决方法问题来源据数学家、历史学家Eutocius(6世纪人)叙述,这个问题可追溯到古代的一个传说。希腊数学家、天文学家、哲学家Eratosthenes(约前284~前192)曾在一本书中叙述:有一次,Delos地方瘟疫流行,居民们纷纷祈求神谕,巫神回答说,要想解除灾难,必须博取上帝的怜恤,为此必须把太阳神庙中的立方体形金祭坛的体积增加一倍。于是居民们立即赶制了两个同样大小的金祭坛送到庙中,把一个叠在另一个的上面,以为这样就满足了把祭坛体积扩大一倍的要求。岂料瘟疫继续流行,居民们只得再去祈求神谕,“我们已经把金祭坛增大了一倍,为什么瘟疫还不停止流行?”巫神回答说,“不,你们没有解决所提的问题,你们必须把金祭坛加大一倍,但不能改变立方体的形状”。居民们解决不了这个问题,便去请教数学家、哲学家柏拉图,柏拉图搪塞地回答:“大概上帝不满意你们很少研究几何学吧!”但柏拉图自己也未能解决这个作图问题,这实际是个尺规作图不能问题。
这当然是一个民间传说,也许纯属虚构。不过,故事中提到的那个数学问题,却是一个举世闻名的几何作图难题,叫作立方倍积问题。
解决方法设已知立方体的边长为a,求作立方体的边长为x,则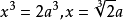 ,若取
,若取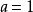 ,则
,则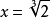 。因此原问题可归结为:“能否用尺规作出长为
。因此原问题可归结为:“能否用尺规作出长为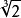 的线段?”3。
的线段?”3。
最早公开申明长为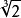 的线段不能用尺规作出的是法国的笛卡尔。1637年,他提出了一个命题:非立方有理数的立方根不能简化为有限次的开平方,从而不能用尺规作出。用尺规不能解立方倍积问题的严格证明,是法国数学家Wantzel在1837年给出的。
的线段不能用尺规作出的是法国的笛卡尔。1637年,他提出了一个命题:非立方有理数的立方根不能简化为有限次的开平方,从而不能用尺规作出。用尺规不能解立方倍积问题的严格证明,是法国数学家Wantzel在1837年给出的。
但是,如果允许使用某种辅助工具的话,立方倍积问题还是可以解决的,在林鹤一的《初等几何学作图不能问题》一书中,介绍了10种方法。
希腊数学家Menaechmus(约前375~前325)的方法是利用两条抛物线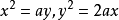 ,因为其交点的横坐标满足
,因为其交点的横坐标满足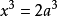 。
。
笛卡尔的方法是利用抛物线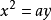 和圆
和圆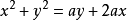 的交点。
的交点。
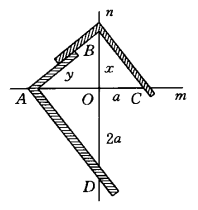
柏拉图的方法是利用两根普通的直角尺。如图1,取相互垂直的两直线m和n,交点为O,在直线m上取OC=a,在直线n上取OD=2a。将两根木匠用的直角尺按图所示放置,使一根尺的一边(内侧)经过点C,而直角顶点B(内侧)在直线n上;使另一根直角尺的一边(外侧)经过点D,而顶点A(外侧)在直线m上,然后使两根尺子的另两边重合。这时,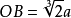 (若
(若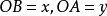 ,则
,则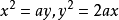 ,从而
,从而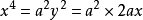 ,即
,即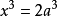 )。
)。
最简单的是如下纸条作图法:
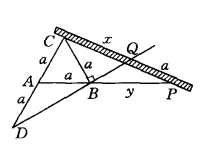
(1)画一个边长为a的正三角形ABC,延长CA到D,使AD=a,作出DB线;
(2)取一笔直的纸条,在其边缘上标出距离a;
(3)按如下方法放置纸条,使纸条的边缘通过点C,并使所标线段的两个端点(P点和Q点)分别落在AB和DB的延长线上(见图2),这时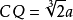 。
。
其理由如下:直线DBQ截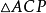 ,根据梅内劳斯定理,有
,根据梅内劳斯定理,有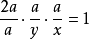 ,即
,即
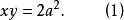
由于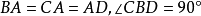 ,利用勾股定理,得
,利用勾股定理,得
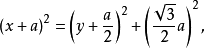 即
即
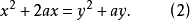 由(1)、(2)消去y,得
由(1)、(2)消去y,得
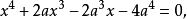
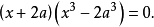
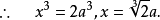
本词条内容贡献者为:
胡启洲 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国