[科普中国]-物理试验设计

物理试验设计是指借助于物理学的知识，首先通过量纲分析法确定指标项与因子项，然后进行实物试验以寻求经验公式或最佳条件的试验设计方法。量纲分析法是物理试验设计的根本方法，通过分析可以使问题简化(减少试验因子和试验次数)，从而减少工作量1。

基本概念所谓物理试验，是指借助物理学的知识，首先通过量纲分析法，确定指标项与因素项，然后进行试验，从而寻求经验公式或最佳条件，它是经过物理分析和实物试验之后完成的，所以叫物理试验法2。

物理量和它的量纲式由物理学可知，物理量分为基本量和导出量，物理公式在确定物理量的数量关系的同时，也确定了物理的单位关系。因此，只要确定几个基本量的单位，就可以推导出其他物理量(导出量)的单位。

在国际单位制(SI)中所确定的基本物理量(基本量)有：长度、质量、时间、热力学温度等，其相应的单位是m(米)、kg(千克)、s(秒)、K(开[尔文])等。在运算过程中，这些基本量的量纲又可分别用符号L、M、T、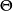来表示。

任何物理量都可以用基本量来表示。表示一个物理量是由哪些基本量组成和怎样组成的式子叫做该物理量的量纲****式。在量纲式中所带的各个指数，就是该物理量对于所取基本量的量纲。例如，某物理量Q的量纲式为

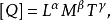
其中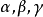分别叫做物理量Q对于长度、质量和时间的量纲2。

量纲分析为了进行量纲分析，先研究简单的物理力程。例如，质点运动方程

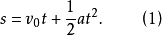也可以写成

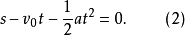或者

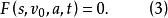
在方程(2)中，每一项的单位都是位移量单位，在量纲分析中，称这种方程为量纲齐次式2。

假设以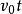t除(2)式，则可写成

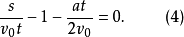
或

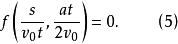
在这里可以看到：方程(5)中的两项代表无量纲的量，而且由原来存在4个物理量的表达式，演变成两个无量纲的量的表达式。

一般可将原来的物理方程表示为

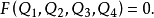
若用无量纲量表达，则为

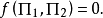推而广之，可写成

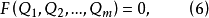
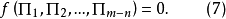
在这里可以看到，无量纲量表达式的项数，总是比原来物理方程中的物理量的项数少，量纲分析法的最大优点，就在于此。它可以应用较少的参数来描述某一关系，从而简化实际问题2。

例题分析例1 设简支梁的最大挠度为d，长度为l，粱的材料弹性模量为F，截面积对中性轴的惯性矩为I，在梁长度的中点所受的集中载荷为P。试求无量纲项，并指出其项数2。

在本例中，现有的物理量为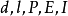共五项，即m=5；而基本量为L，M，T共三个，即n=3，所以，无量纲组数为m--n=2。

由物理知识可知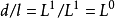，，是一个无量纲数，所以第一个无量纲组为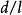；另一个无量纲组可以设定，设为

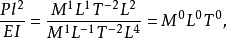这就是量纲分析所得到的结果。

量纲分析虽然结束，但并未求出两个无量纲组之间的关系，更未得到所需的理论公式。为了求得两个无量纲组之间的关系，可假设

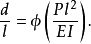这样，便可以把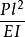当做一个因素，然后取若干水平进行试验，把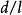做为指标，试验后便可得到二者关系。

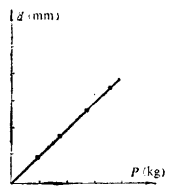
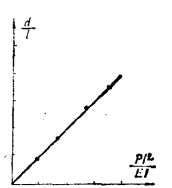
本例中作出的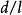与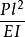间的关系曲线如图1（b）所示。最后得到的关系为

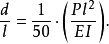或

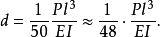这个结果与理论分析推导出来的结果非常接近。

由此可见，通过量纲分析，不论从理论方面还是从试验方面，其工作量都大为减少。假如不用量纲分析法，试验设计时，把梁的挠度d做为试验指标，把影响挠度的因素包括梁的长度l、弹性模量E、截面矩I，和载荷p做为因子，则需设计多因素多水平的试验，就需要用多个不同的梁，加上不同的载荷，进行许多次的试验。而用量纲分析法，则只需一条简支梁进行单因素试验即可完成2。

π定理——白金汉定理上述方程中的两个无量纲组，都是根据专业知识设定的。但是，在一般情况下，究竟怎样寻求无量纲组的组数和无量纲组形式呢?这就要用量纲分析法中的一个主要定理——π定理(或称白金汉定理)。其内容如下： “设有m个物理量用n个基本量表示为量纲表达式，同时，m个物理量有关地存在于一个齐次量纲物理方程中，则m令物理量可用(m-r)个无量纲乘积表示，而r(≤n)在这里为m个物理量所组成的矩阵之秩”2。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所