戴德金原理(Dedekind principle)亦称戴德金分割,是保证直线连续性的基础,其内容为:如果把直线的所有点分成两类,使得:1.每个点恰属于一个类,每个类都不空。2.第一类的每个点都在第二类的每个点的前面,或者在第一类里存在着这样的点,使第一类中所有其余的点都在它的前面;或者在第二类里存在着这样的点,它在第二类的所有其余的点的前面。这个点决定直线的戴德金割切,此点称为戴德金点(或界点),戴德金原理是戴德金((J.W.)R.Dedekind)于1872年提出来的,在构造欧氏几何的公理系统时,可以选取它作为连续公理,在希尔伯特公理组Ⅰ,Ⅱ,Ⅲ的基础上,阿基米德公理和康托尔公理合在一起与戴德金原理等价1。
基本介绍定义1 若将实数集R分成两个子集S和T,它们满足:
(1)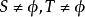 ;
;
(2)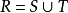 ;
;
(3)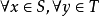 ,总有x0,且x2>2)则(S,T)构成对有理数集Q的戴德金分划,但左集S无最大数;右集T无最小数,也就是(S,T)没有中介点2。
,总有x0,且x2>2)则(S,T)构成对有理数集Q的戴德金分划,但左集S无最大数;右集T无最小数,也就是(S,T)没有中介点2。
戴德金原理 实数集R的任一戴德金分划(S,T),都唯一地确定一个实数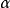 (称为中介数或中介点),它或者是S的最大数(此时T中无最小数)、或者是T的最小数(此时S中无最大数)。
(称为中介数或中介点),它或者是S的最大数(此时T中无最小数)、或者是T的最小数(此时S中无最大数)。
戴德金原理的证明在S中任取一数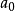 ,T中任取一数b0,由戴德金分划的“不乱”性质,
,T中任取一数b0,由戴德金分划的“不乱”性质,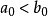 ,闭区间
,闭区间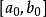 的左端点属于S;右端点属于T,这样的闭区间称为入选区间,把
的左端点属于S;右端点属于T,这样的闭区间称为入选区间,把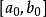 二等分,设中点为c,则
二等分,设中点为c,则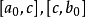 中必有一个且只有一个是入选区间,把它记作
中必有一个且只有一个是入选区间,把它记作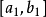 ,再把
,再把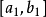 二等分,而得到第三个入选区间
二等分,而得到第三个入选区间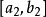 ,……这样进分下去,便能得到一个入选区间组成的序列
,……这样进分下去,便能得到一个入选区间组成的序列
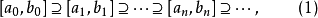 因为这是逐一二等分得到的序列,所以
因为这是逐一二等分得到的序列,所以
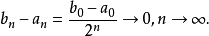 可见序列(1)是一个退缩闭区间套,据退缩闭区间套定理,存在唯一实数
可见序列(1)是一个退缩闭区间套,据退缩闭区间套定理,存在唯一实数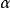 ,使
,使
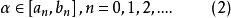 下面证明
下面证明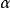 便是中介点2。
便是中介点2。
设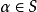 ,如果
,如果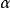 不是S的最大数,则必存在实数r∈S,使
不是S的最大数,则必存在实数r∈S,使
 又由于对每个n,bn∈T,而r∈S,所以
又由于对每个n,bn∈T,而r∈S,所以
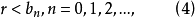
由于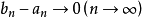 ,故对充分大的n,必有
,故对充分大的n,必有
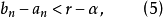 对于端点满足(5)式的闭区间
对于端点满足(5)式的闭区间 ,必有
,必有
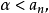 即
即
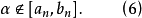 否则,如果
否则,如果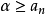
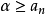 ,与(3),(4)两式联立起来,将有
,与(3),(4)两式联立起来,将有
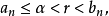 将得到
将得到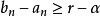 ,与(5)式矛盾。但(6)式是与(2)式矛盾的。这个矛盾说明假设
,与(5)式矛盾。但(6)式是与(2)式矛盾的。这个矛盾说明假设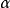 不是S的最大数是不对的,
不是S的最大数是不对的,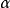 必为S之最大数。
必为S之最大数。
S中有最大数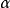 ,T中必无最小数,否则,若T中有最小数
,T中必无最小数,否则,若T中有最小数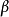 ,则
,则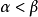 。由实数之稠密性,存在实数
。由实数之稠密性,存在实数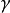 ,使
,使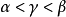 ,但
,但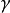 既不是S中的元素(因
既不是S中的元素(因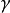 >S中的最大数),又非T中的元素(因
>S中的最大数),又非T中的元素(因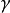




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国