[科普中国]-黎曼几何模型

黎曼几何模型(model of Riemannian geometry)是解释黎曼几何的模型，在射影平面上取一条非退化的虚二阶曲线Γ：x²₁+x²₂+x²₃=0作为绝对形，若以射影平面上的点为点，直线为直线，在距离的射影测度d(A，B)=kln(AB，PQ)中取k=iα/2，在夹角的射影测度w(a，b)=kln(ab，pq)中取k=i/2，则在这个模型里，不存在不相交的直线，所以过直线外的点不存在与已知直线共面而不相交的直线，且三角形内角之和大于π，这就是黎曼几何的一个模型1。

我们知道欧氏几何与罗氏几何的主要分歧点在于平行公理的截然相反，现在把它并列起来比较一下：

欧氏平行公理；“在平面内，过已知直线外的一个已知点，最多只能作一条直线与已知直线平行(不相交)”。

罗氏平行公理：“在平面内，过已知直线外的一个已知点，最少可以作两条直线与已知直线不相交。”并进一步指出有无数条超平行线都与已知直线不相交。

经过比较，我们很自然地会问：是否有这样的几何，在平面内，过直线外的一个已知点与已知直线不相交的直线一条也没有呢?这种“最多一条”，“最少两条”，“一条也没有”的联想，必然会在人们的脑子里反映出来。

另一种联想是：在欧氏几何里，三角形的内角和等于二直角；在罗氏几何里三角形内角和小于二直角；是否有一种几何它的三角形内角和大于二直角呢?

历史的发展回答了这个问题。

当罗巴切夫斯基发表罗氏平行公理的论文28年后；德国数学家倍耳哈特·黎曼(Bernhard Riemann，1826-1866)在1854年发表了既不属于欧氏也不属于罗氏，而是自成体系的“黎曼几何”。

黎氏平行公理：“任何两条直线必有唯一的交点”。

同时，黎氏几何中还指出：任何直线虽然可以任意伸长，但长度是有限的。

这个事实可以用一个欧氏的球面略加改造，作为黎氏几何的模型来作解释2。

下面是黎氏几何模型的规定：

规定1 在欧氏空间中任取一个球面K，约定把球面上的对径点(球直径的两端点)“统一起来”，看作一个对象，这个对象便叫做黎曼几何的“点”。

规定2 球面K上的大圆叫做“黎氏直线”，大圆上的对径点仍看作一个点。

规定3 对经点统一起来的球面K，叫做“黎氏平面”。

规定4 所谓黎氏点和黎氏直线的结合关系，就是球面K上的点与球面K上的大圆弧的普通结合关系。

由于在球面K上，任何两个大圆必相交于两个点，而这两个点恰好是对径点，把它看成一个点，所以说黎氏平面上任何两条直线必相交于一个点，这样就实现了黎氏平行公理2。

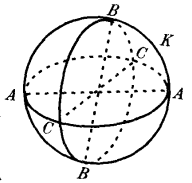
另一方面，大圆上任一点，可沿大圆弧任意移动，但大圆的长度是有限的，所以说黎氏直线可以任意伸长，但是有一定的长度。

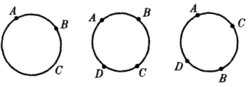
应当注意，关于点的顺序公理，必须要有所规定。因为大圆弧上的A、B、C三点。B可以在A、C之间，C可以在B、A之间；A可以在C、B之间。因此必须要用四个点，才能说明顺序关系，分两种情况说明：

1. 点对A、B分离点对C、D。意思是说，点C沿着直线移动，使之与D重合，则必须在某个时候，C与A或B重合，要使A与B重合也一样，即A必先与C或D重合。

2. 点对A、B不分离点对C、D。这时，可以移动点C，使之与D重合，但不必通过A或B；同时也可以移动点A使与B重合，而不通过C和D。

所以必须要四个点，才能说明顺序关系，直线的分离关系也是一样。

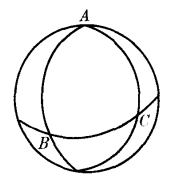
从球面几何知识：任意三条大圆弧围成的球面部分，称为球面三角形(如图ABC)。它的内角和是大于二直角的，这就证实了黎氏平面上三角形内角和大于二直角2。

我们又知道在罗巴切夫斯基平面内，三角形的面积

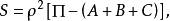或

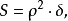(这里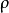是罗氏曲率半径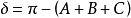，是角亏。)

如果用 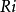换替上式中的，

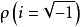那么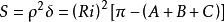

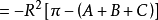
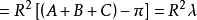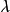(是角余)。

所以，在罗氏几何中，如果把曲率半径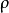换成Ri的话，就得到黎氏几何中的面积公式。这个变换不仅是十分有趣的，而且也说明了罗氏几何和黎氏几何之间的一种关系，给我们研究黎氏几何开辟了一种新的途径。

在这里，还要指出一个十分有趣的性质：任意一条直线不能把黎曼平面分成两个不同的区域，例如大圆a，初看似乎把球面K分成Ⅰ、Ⅱ两部分了，似乎A点落在Ⅰ域。但不要忘记，我们是规定把A的对径点A1看成同一个点的。而这时的A1是在Ⅱ区域，即A点是区域Ⅰ的点，也是区域Ⅱ的点。因此，直线a并没有把黎曼平面分成两个不同的区域。

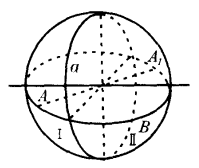
同时，我们也看到，Ⅰ、Ⅱ两部分的点A和B，可以用不与a相交的直线段连结起来，因为A的对径点A1就是A点。很明显，直线段A1B是不与直线a相交的。

黎曼平面的这种特殊性质，用拓扑学上的名词来说，称为单侧性。梅比乌斯带子也是具有单侧性的。

关于黎曼几何的知识，这里只粗略地谈一些易于接受的内容，读者如果还想进一步探讨，可参阅钱端壮编著的《几何基础》第六章《黎曼几何学》2。

本词条内容贡献者为: