[科普中国]-郎之万-德拜公式

本世纪初,Langevin和Debye提出了顺磁性的经典理论.在量子力学出现后,VanVleck发展了顺磁性的量子理论.在此基础上,1932年,他导出了原子或离子系统磁化率的普遍公式,这就是广义的Langevin-Debye公式,简称为Langevin-Debve 公式。

推导过程

考虑原子磁矩不为零的系统，当磁场不十分强时，同样用微扰方法求出体系的能量，（只保留到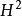 项）

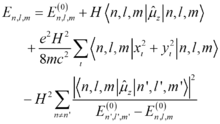
这里与原子磁矩为零时的区别就在于对原子磁矩不为零的系统原子，微扰中的一阶项不再等于零。

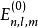是基态能量，后面三项是微扰能量 ，在微扰能量远小于基态能量和平均热动能的情况下，（相当于弱磁场或高温情形，可以不考虑顺磁饱和现象）给出体系的状态和，求出系统的磁化率。

玻尔兹曼统计的配分函数为：

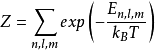
系统的磁化率为：

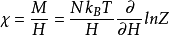
其中 N 为单位体积的原子数,取：

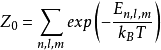
可以计算出顺磁磁化率的表达式为：

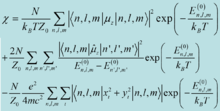
该式称作朗之万- 德拜公式，其中第三项就是前面给出的抗磁磁化率项。头两项是顺磁磁化率，第一项是取向顺磁磁化率，和朗之万经典结论相似，与温度有关。

第二项是激发态对顺磁性的贡献，与温度基本无关。一般情况下比第一项小得多，称之为：范弗莱克（Van Vleck) 顺磁性。

对范弗莱克顺磁性的一些理解

在近似计算自由原子（离子）的顺磁性时，我们忽略了磁场对本征波函数的作用，然而事实上， B≠ 0 时的本征波函数不同于B = 0 时的本征波函数，B≠ 0 时的本征波函数是B = 0 时未受扰的一些本征波函数的组合，结果使非干扰状态的磁矩发生变化，这种作用对磁化率的贡献首先是范弗莱克用微扰理论计算出来的，也称为范弗莱克顺磁性1。

Van Vleck 顺磁性来源于磁场对电子云的形变，即二级微扰使激发态混入基态，使电子态发生微小的变化所致，它常是对顺磁性和抗磁性的一个修正，且基本不依赖于温度2。

范弗莱克量子理论很好的揭示了过渡族元素和稀土族元素间的差异，并指出稀土元素 Sm+3和Eu+3 的特殊性，揭示了它们的原子磁矩偏离洪德法则的原因。

虽说原则上可以利用范弗莱克量子理论计算任何原子的磁化率，但实际上是很困难的，需要繁琐而复杂的量子力学计算。

小结： 范弗莱克量子理论正确处理了顺磁性和抗磁性的问题，揭示了它们之间的内在联系，指出了除去原子磁矩的取向效应外，还存在一个与温度无关的顺磁效应——范弗莱克顺磁性。

他既肯定了 Langevin 经典理论正确的一面，又指出了经典理论的不足，成功地解释了复杂多变的实验结果34。

具体的讲，范弗莱克量子理论的结果，按激发能量 Δ 的大小可以区分为如下三种不同的情况：

（1）当 Δ > kBT 时，激发态能量很高，离基态较远。这时，大部分原子仍处在基态。可以证明：这时激发态的影响将导致一项与温度无关的顺磁化率。

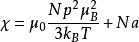这里的第二项称为范弗莱克顺磁性，它与温度无关，是量子理论的结果。大多数稀土离子属于这种情况。p 的理论值与实验基本符合。

（3）当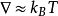 时，激发态离基态不远。这时磁化率与温度的关系比较复杂，不同于居里定律的形式。稀土离子 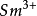和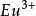就属于这种情况。用 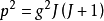的计算结果与实验相差较大。

本词条内容贡献者为:

韩拯 - 研究员 - 中国科学院金属研究所