[科普中国]-托里切利点

托里切利点(Torricelli point)是三个具有特殊位置的圆的交点。在△ABC的三边上各向外侧作等边三角形ABC₁，BCA₁，CAB₁，这三个等边三角形的外接圆交于一点T，这一点T称为△ABC的托里切利点，这三个外接圆称为托里切利圆。当△ABC的三内角都小于120°时，△ABC的托里切利点T具有性质：它到三个顶点距离之和AT+BT+CT达到最小。求一个到三角形三个顶点的距离之和为最小的点这个问题是由费马(Fermat，P.de)提出而由托里切利(E.Torricelli)解决的，所以托里切利点也称为费马点1。

基本介绍在三角形ABC的三边AB、BC、CA.上，各向外侧作等边三角形ABC₁、A₁BC、AB₁C，这三个等边三角形的外接圆交于一点T，我们把点T叫做这一三角形的托里拆里点，而把这三个外接圆叫做托里拆里圆2。

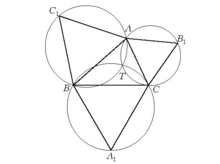
当三角形的三个内角都小于120°时，三角形ABC的托里拆里点T具有如下性质：它到三个顶点的距离之和AT + BT+ CT达到极小。

托里拆里(E.Torricelli, 1608~1647)是意大利物理学家，在一定条件下，托里拆里点和正等角中心、费马点是一回事，只是托里拆里点是由共点圆来提出问题的，而正等角中心是由共点线来提出问题的，费马点则是由几何极值来提出问题的2。

托里切利托里切利(Torricelli，Evangelista)(1608-1647)

托里切利是意大利数学家、物理学家。1608年10月15日生于法恩扎；1647年10月25日卒于佛罗伦萨3。

托里切利出生于贵族家庭。1628年开始在罗马学习数学。在伽利略的著作启发下，他写了一篇论文《运动论》，论文引起了伽利略的注意。1641年被邀请到佛罗伦萨会见已经双目失明的伽利略，并在伽利略生命的最后三个月成为他的秘书和朋友。1642年伽利略去世后，他继伽利略之后成为佛罗伦萨的宫廷数学家。

托里切利对几何学的研究促进了微积分的发展，他充分认识到不可分量方法的优点及缺点。他写的《关于抛物线的维数》是一本很有价值的著作。对抛物线的求积，他提出21个证明，其中10个证明是用古人的方法，其它11个则用了新的不可分量的几何方法。他在使用不可分量的方法时发现了许多新的结果，并且在灵活和透彻性方面胜于卡瓦列利。托里切利的工作把前人和同时代人所提出的思想和方法，运用得十分精练与娴熟，以致他的名字在许多情况下都成为争论优先发明权的焦点3。

托里切利还用运动合成来确定任意正整数次幂的抛物线的切线。把这种方法用到瞬时方向的思想，隐含了极限的概念。他通过把瞬时速度的概念渗透到几何证明中去，从而跨越了经典的传统论述。他还采用运动合成法求出了阿基米德著作中所提出的一大类曲线的切线。托里切利用几何方法证明了，一门大炮以相同的初速，但以不同的仰角发射的炮弹的弹道之包络是一条以炮位为焦点的抛物线。

从托里切利对穷竭法、不可分量法、运动合成法的综合应用中， 可以发现许多类似于微积分的结论，其中有求曲线弧长、求曲边形面积、求曲线的切线的一些定理。例如，他证明了：摆线一拱下的面积正好是母圆面积的3倍。特别是，他好象已经认识并应用了：“求切线问题是求面积问题的逆运算”这一规律。遗憾的是，他没有再前进一步，在这些方法的基础上建立起普遍适用的一般法则。因而他的工作只差一步便迈进了微积分的重要领域。

托里切利还研究过摆线的性质。他得出了：如果分别以三角形ABC的三条边AB、BC、CA为边， 各向此三角形的外侧作正三角形ABC₁、A₁BC、CB₁A，则这三个正三角形外接圆交于一点，这个点称为所给三角形的托里切利点。

托里切利对物理学的突出贡献是：在《几何运算》(1644年)一书中，他把动力学的若干著名原理推广到流体方面；研究过水从容器壁上小洞流出的流量问题；证明了现代教科书上的托里切利原理；对睛雨计的研究使他能把经院哲学中“大自然畏惧真空”这个幽灵赶走，他对玻璃管中为什么能支持水银柱的现象给予正确的解释，并提出可以利用水银柱高度来测量气压。1644年他同维维亚尼(Viviani)：合作制成了世界上第一具水银气压计，一个大气压力相当于760毫米高的水银柱的压力。为了纪念托里切利，将1毫米水银产生的压强定义为1“托”。托里切利研究抛物体运动时，不但得出了抛物体的轨迹是一条抛物线， 而且还猜想出，与水平线成45°角的抛射可以达到最大射程3。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所