[科普中国]-比例线段法作图

比例线段法作图(constructing by proportional segments)是一种常用的作图方法。利用比例线段的有关定理解作图题，称为比例线段法作图。

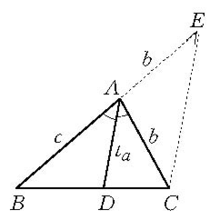
基本介绍在求线段长度的计算题中，有许多要利用比例线段定理求解．这样的方法我们称为比例线段法。例如，已知两边b，c及b，c夹角的平分线ta，求作三角形。其思路要点是：如图1，假设△ABC为所求，即AB=c，AC=b，∠A的平分线AD=ta，延长BA至E，使AE=b，连结EC，因而AD∥EC，所以利用成比例线段AD/EC=BA/BE，EC=ta(b+c)/c，于是△ACE可作出并成为奠基三角形(如图1)，当ta同时大于或等于b，c时，本题无解，否则有一解1。

例题解析下面讨论将线段比例的性质运用到几何作图中去的方法。

首先指出，两线段的比，根据定义是“用同一长度单位去量两线段所得的量数之比”。所以四条线段组成的比例实际上是它们四个量数两两之比所组成的等量关系。因此，关于数的比例的各个性质，也适用于线段的比例2。

【例1】求作一个三角形与已知三角形相似，且使它的面积等于已知三角形面积的九倍。

已知△ABC，

求作三角形：与△ABC相似，面积是△ABC面积的九倍。

分析设△EFG符合条件: △EFG∽△ABC，S△EFG=9S△ABC。

因为相似三角形面积的比等于对应边的平方比，设与边AB对应的边是EF，则有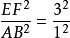，所以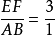，EF=3AB。EF可以作出，再根据相似形的性质，可以作出△EFG。

作法 ①作EF =3AB。

②作∠GEF=∠CAB，作∠GFE=∠CBA，EG、FG交于G。

△EFG就是所求作的三角形，图2。

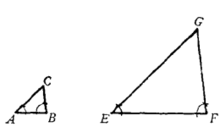
证明 ∵∠E=∠A，∠F=∠B (作图)，

∴ △EFG∽△ABC，

又：EF= 3AB，即 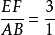(作图)，

而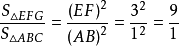(相似形性质及等量代换)，

∴

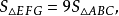
∴ △EFG符合条件。

讨论 仅有一解2。

【例2】已知两线段的f和，又知它们的比例中项，求作该两线段。

已知 线段l、f，且I= m+ n，f²= m**.**n，

求作 线段m、n。

分析 考虑到直角三角形中斜边上的高是斜边被垂足分成的两条线段的比例中项，如果将斜边取成l，高取成f，则被垂足分成的两条线段就分别是m,n。

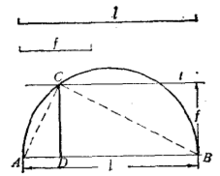
作法 ①作AB=l，以AB为直径画半圆。

②作直线t // AB 交半圆周于C，且使t与AB间的距离等于f 。

③过C作CD⊥AB交AB于D，

则AD= m，BD =n(或AD=n，BD=m) (图3)。

证明 连AC、BC。

∵∠ACB是半圆周上的圆周角，

∴∠ACB= 90°，

∵CD⊥AB (作图)，

∴CD²= AD**.**BD (直角三角形斜边上的高是斜边被垂足分成的两条线段的比例中项)，

但CD= f (平行线间的距离处处相等)，

∴AD**.**BD=f²，

又 AD+BD= AB=l(作图)，

AD= m，BD=n(或AD=n、BD= m)。

讨论 问题之有解无解取决于t与半圆周交点存在与否。如果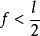，，有两个交点，有二解，这时m≠n；如果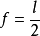，有切点，这时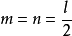，一解；如果，t与半圆周无交点，又不相切，无解2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学