[科普中国]-热尔岗点

热尔岗点(Gergonne point)是三角形三条特殊直线的交点，若X，Y，Z分别是△ABC的三边BC，CA，AB与其内切圆或旁切圆的切点，则三线AX，BY，CZ共点，这样的点共有四个，称它们为△ABC的热尔岗点。热尔岗点的等截共轭点称为△ABC的奈格尔点1。

基本介绍热尔岗定理 分别连接三角形一个顶点及对边上的内切圆切点的三条直线共点。

这个点被称为此三角形的热尔岗点。

热尔岗点的证明证明 在图1中，圆O与AB、AC、BC三边分别相切于N、M、L三点。

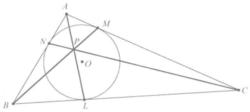
由此可得AN=AM，BL=BN，CM=CL。这些等式可以写成

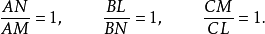将这三个分式相乘，我们就得到

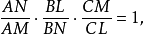因此，

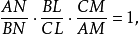由切瓦定理得，AL、BM和CN共点。这个点就是△ABC的热尔岗点2。

相关结论⑴ 三角形的内切圆切于BC，CA，AB三边于D，E，F三点，则AD，BE，CF交于一点，该点称为热尔岗(Gergonne)点，以Ge记之。

类似地，三角形三个旁切圆在BC，CA，AB三边上的切点，分别是D'，E' ，F' ，则AD'，BE' ，CF'交于一点，该点称为奈格尔(Nagel)点，以Na记之。

⑵ 现在把内切圆与旁切圆统一联系起来，设在BC边上两个圆的切点分别是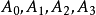;在AC边上两个圆的切点分别是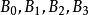;在AB边上两个圆的切点分别是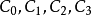，则有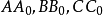交会于Ge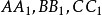，交会于G1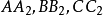，交会于G2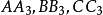，交会于G3，这是四个热尔岗点。

又有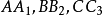交会于Na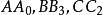，交会于N₁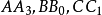，交会于N₂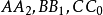，交会于N₃，这是四个奈格尔点。

⑶ 三角形诸热尔岗点及纳格尔点的等角共轭点分别是外接圆与内切圆及外接圆与旁切圆的相似中心。

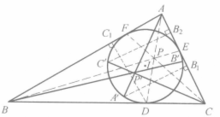
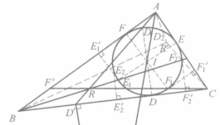
证明 如图(a),设D,E,F关于AI,BI,CI的对称点为A',B',C',则不难知AA',BB',CC'为AD,BE,CF的等角线,所以AD,BE,CF交于P(热尔岗点)的等角共轭点为P'(AA',BB',CC交点)。

因为A'B₁=DC₁,C'B₂=EA₁,DC₁=EA₁,所以A'B₁=C'B₂,故A'C'//AC,同理C'B'//CB,B'A'//BA,所以三角形A'B'C'与△ABC关于P'位似,故⊙I与⊙ABC也关于P'位似，即⊙I与⊙ABC相似中心为P'。
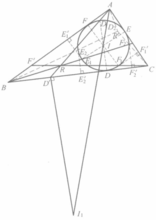
如图(b),设ID,IE,IF交⊙I于另一点D₁,E₁,F₁,则不难导出AD₁,BE₁，CF₁为AD,BE,CF的等截线,所以AD₁,BE₁,CF₁交于一点R(纳格尔点)。
设D₂,E₂,F₂是D₁,E₁，F₁关于IA,IB,IC的对称点，有AD₂,BE₂,CF₂为AD₁,BE₁,CF₁的等角线，因此它们必交于一点R'(R的等角共轭点)3。

⑷ 热尔岗点有一个有趣的推广。

定理△ABC的内切圆切BC，CA，AB于D，E，F三点，另作一与内切圆的同心圆⊙R，ID,IE,IF的延长线交⊙R于D'，E'，F'，则AD'，BE'，CF'三线共点 (图3)。

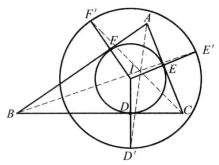
⑸ 原三角形中的热尔岗点也是下列三角形中的几何特征点：内切点三角形中的共轭重心；反补三角形中的M点；内心垂足三角形中的共轭重心；垂心的反垂足三角形中的M点；内切点三角形中的余弦圆圆心等等。

|| || 表1是透视或位似中心为热尔岗点的三角形对列表

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所