[科普中国]-等角半正多面体

等角半正多面体(equiangular semiregular polyhedron)亦称阿基米德多面体，是一种特殊的多面体，指所有多面角都相等，且各个面是边数不全相同的正多边形的多面体，等角半正多面体的多面角最多有五个面，侧面是正方形的正n棱柱是等角半正(n+2)面体，又如取正n面体(n=6或8，12或20)各棱的中点作为顶点所成的多面体也是等角半正多面体，分别称为立方八面体或中央晶体(由六个正方形和八个正三角形围成的)和十二兼二十面体(由十二个正五边形和二十个正三角形围成的)1。

基本介绍如果多面体的面是由几种不同的正多边形组成，而它们的多面角都相等，这样的多面体叫做等角半正多面体。如果多面体的多面角是几种不同的角度而各面都相等，这种多面体就叫做等面半正多面体2。

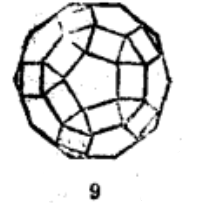
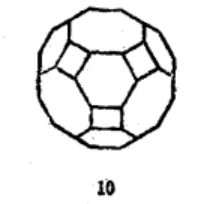
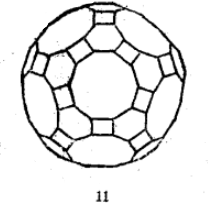
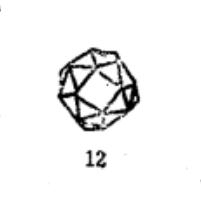
三维空间中共有十三种等角半正多面体(见表1)。半正多面体是由正多面体演变得来的。

|| || 表1 十三种等角半正多面体

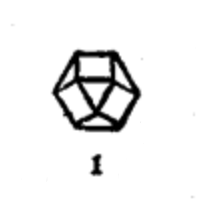
如果把正四面体的各棱中点同一组线连接起来，就可以发现这组线构成了一个正八面体。同法，把六面体或八面体的各棱中点连线，结果是一个立方八面体，把十二面体或者二十面体的各棱中点连线，结果叫做十二兼二十面体(见图1)。由此可知，正多面体各棱中点连线可生成八面体、立方八面体和十二兼二十面体。正是由于中点将各棱分成两段，因此又称这三种形体为二次形体2。

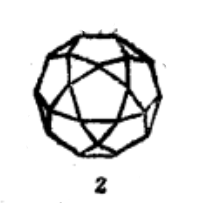
如果将三多面体的各棱不是分为两段而是分为三段，和前法相同用一组线把这些分点连接起来，则五种正多面体即演变出截顶四面体、截顶八面体、截顶六面体、截顶二十面体和截顶十二面体。由于这五种形体是分割正多面体各棱为三段而形成，故又叫做三次形体(见图2)2。

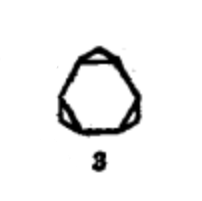
如果将二次形体的各棱分为两段，用一组线连接起来即形成四次形体(见图3)。四次形体中出现两种新的形体一小的正交立方八面体和小的正交十二兼二十面体。因为立方八面体和十二兼二十面体的演化物具有矩形的面，它的棱长不等，必须有少量扩大，把矩形变成正方形，从而使各面的棱长相等，当用这种方法扩大形体时，其两面角大小不变。

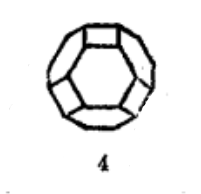
如果是将二次形体的各校分为三段，用一组线连接起来即为六次形体(见图4)。六次形体中衍生出两个新的形体——大的正交立方八面体和大的正交十二兼二十面体2。

等角半正多面体的一些特征等角半正多面体的一些特征2：

1.形体上每个多面角相等

半正多面体的面和正多面体一样，是由正多边形组成，不同的是正多面体的所有面是同一种类型的正多边形，而半正多面体却是两种或两种以上类型的正多边形面。由于各种形体在每一顶点处的面是同样规律排列的，所以它的每一顶点处的面角和必定是一样的2。

正多面体上相邻两面间的二面角是不变量，半正多面体中除了立方八面体和十二兼二十面体的二面角也都是不变量外，其它形体则有两种或三种不同的二面角。举例来说，从一个截顶六面体的模型来看，其两个相邻的八边形的二面角是90°,而八边形与其相邻的三角形间的二面角虽然是不变量，但很明显它不是90°，实际上是125°16'。

2.半正多面体都有一个外接球和一个内接球

由于每个半正多面体可以外切于一个正多面体，因此它的所有顶点都均匀地位于其外切形体的棱或面上， 例如一个立方八面体和一个大的正交立方八面体外切于一个六面体。见图5(a)和(b)。在每种情况中，内接形体的顶点和外切形体内的中心距离是相等的，因为从形体中心到每个正多阿体的面的中心是一个固定的距离，由形体的中心到内接形体的顶点也是一个固定的距离，因此半正多面体和正多面体一样，具有一个外接球，它的所有顶点与其相接触。再次，由于半正多而体的所有棱长相等，对它的外接球来说也是具有相等的弦长，从外接球中心到弦的中点距离相等，因此半正多面体像正多面体一样有一个内接球与所有棱相接触。但是，由于半正多面体的顶点或棱到不同类型的面的中心距离不是一个定值，从截顶八面体的六边形或正方形即可看出[图5中的(c)]，所以，和正多面体不同，半正多面体不能作一个内球与各面相接触。

3.半正多面体的面角总和

在正多面体的一些特征中已经说明，由平面构成的任何一个凸多面体面角的总和永远是360°×顶点数-720°，用此公式去检验一个半正多面体也是一一样的。

例如，立方八面体有十二个顶点，按照公式它的面角总和等于360°×12-720°，即3600°。这个形体有八个三角形面，每一个面的内角总和是180°， 八个三角形的面角总数是1440°，它的六个正方形面，每个面的面内角和是360°，六个正方形面的内角总和是2160°，从而三角形和正方形两项面角的总和是(1440°+2160°)3600°。这个公式对任何一个半正多面体都是适用的。

4.每个半正多面体可以外切于一个四面体

等角半正多面体的一个重要特性是可以外切于一个四面体，因此，它有四个面重合在那个四面体的各面上。举例来说，如图6所示，一个截顶八面体的四个六边形面能重叠在四面体的各面。因此，半正多面体的定义是一个凸多面体，它的每个顶点周围有两种或两种以上类型的正多边形，并且它能外接于一个正四面休，它有四个面落在四面体的面上，这样的定义就概括了十三种等角半正多面体2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所