长方台(cuboid frustum)是一种特殊的拟柱体,两底面都是矩形,并且它们的对应边平行的拟柱体称为长方台。
基本介绍两底面是矩形、且对应边平行的拟柱体叫长方台。长方台在中国古代称刍童、盘池、冥谷,并在《九章算术》中给出了它的体积计算公式,其公式是拟柱体体积公式的特例1。
图6中上底长(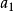 ),宽(
),宽(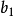 );下底长(
);下底长(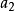 ),宽(
),宽(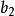 );高(h)为已给,它的体枳公式是
);高(h)为已给,它的体枳公式是
V刍童=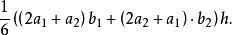
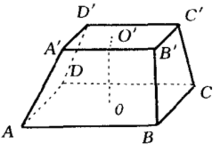
(如图1)这两个矩形的面叫做长方台的底面,如图中的ABCD和A'B'C'D',其余各叫做长方台的侧面如ABB'A'、BCC'B'等,两底面间的距离叫做和长方台的高,如OO',长方台的各侧棱延长后不一定相交于同一点2。
拟柱体 所有顶点都在两个平行的平面内的多面体称为“拟柱体”。其中平行的两个多边形面称为拟柱体的底面,其余的面(一般为三角形、平行四边形或梯形)称为拟柱体的侧面,两底面之间的距离称为拟柱体的高,通过高的中点且平行于底面的截面称为拟柱体的中截面。设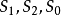 分别为拟柱体两底面和中截面的面积,h为它的高,则其体积是
分别为拟柱体两底面和中截面的面积,h为它的高,则其体积是
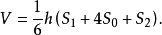 棱柱、棱锥、棱台都可看作拟柱体的特殊情况,它们的体积公式可统一在拟柱体的体积公式中。同样,长方台也是拟柱体,体积也可借此公式计算。
棱柱、棱锥、棱台都可看作拟柱体的特殊情况,它们的体积公式可统一在拟柱体的体积公式中。同样,长方台也是拟柱体,体积也可借此公式计算。
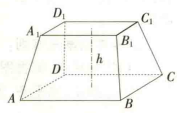
【例1】铸造一个长方台ABCD-A₁B₁C₁D₁如图,上,下底面是互相平行的矩形,相对侧面与底面的夹角相等,已知AB =4,BC=2,A₁B₁=3,B₁C₁=1,高h=2(单位:米),求该长方台的体积。
解法1 (不是棱台——切法) 如图切两次。
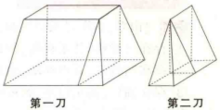
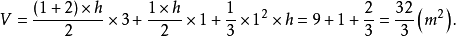
解法2 (用拟柱体计算体积的万能公式)
V拟柱体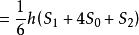
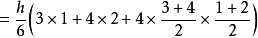
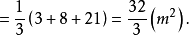
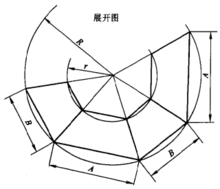
长方台展开计算长方台有锥体长方台和非锥体长方台之分,锥体长方台锥线汇交于一点,非锥体长方台又称敞口矩形台,锥线不汇交一点, 须分别求出各面放样尺寸作出展开图。下面分别加以介绍。
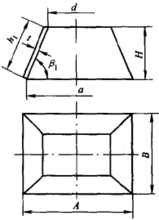
锥体长方台展开计算图4所示为锥体长方台,已知尺寸为A、B、H及h。计算式:
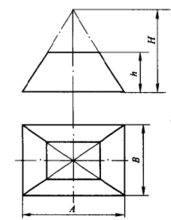
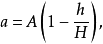
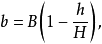
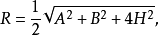
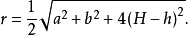
式中 a——矩形台顶口长边;
b——顶口短边。
矩形敞口台展开计算图5所示为矩形敞口台,已知尺寸为A、B、C、D、H及t。
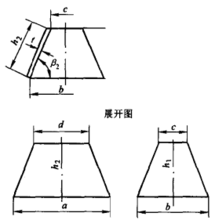
计算式:
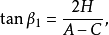
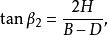
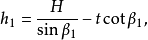
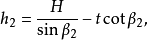
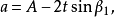
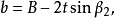
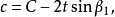
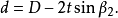
史书记载的长方台体积计算命题 今有刍童,下广二丈,袤三丈;上广三丈,袤四丈;高三丈,问:积几何3?
术曰:倍上袤,下袤从之;亦倍下袤,上袤从之;各以其广乘之;并,以高若深乘之,皆六而一。
答曰:二万六千五百尺。
(《九章算木.商功》第19题)
刍童,中算立体麦用名司,指长方台。
图6中上底长(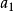 ),宽(
),宽(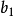 );下底长(
);下底长(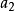 ),宽(
),宽(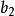 );高(h)为已给,它的体枳公式是
);高(h)为已给,它的体枳公式是
V刍童=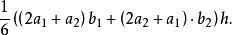
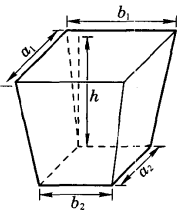
证明 为术又可令上下广袤差相乘,以高乘之,三而一,亦四阳马。上下广袤互相乘,并而半之,以高乘之,即四面六堑堵与二立方,并之为刍童积,又可令上下广袤互相乘而半之,上下广袤又各自乘,并,以高乘之,三而一,即得也3。
(刘徽注刍童术)
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国